044. The Hypergeometric Distribution

The binomial distribution is appropriate only if the Probability of a success remains Constant for each trial. This will occur if the sampling is done from an infinite (or very large) population. The distinction between the binomial and hypergeometric distributions lies in the Population size, especially as it relates to the size of the sample.

If the probability of a success is not constant, if a sample is selected without replacement from a known population and contains a relatively large proportion of the population the Hypergometric distribution is particularly useful.

The Probability function for the hypergeometric distribution is

, (4.16)

Where X is number in the sample identified as a success; N is the population size; R is the number in the population identified as a success; N is a sample size.

Example 4.5. Assume a racing stable has N = 10 horses, and R = 4 of them have a contagious disease. What is the probability of selecting a sample of N = 3 in which there are X = 2 diseased horses?

.

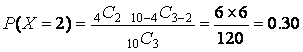There is a 30 percent probability of selecting three racehorses, two of which are ill.

The problem concerning diseased racehorses a hypergeometric coz there are only two possible outcomes: the horses are either (1) diseased or (2) not diseased.

< Предыдущая		Следующая >