038. Two Rules of Probability

The Rule of multiplication is used to determine Joint probability of “A and B” (A∩B). It is states that

1. If A and B are Independent Events, the probability of the event A must be multiplied by the probability of event B.

P(A and B) = P(A) x P(B) , (4.3)

2. If A and B are Dependent events, the probability of the event A must be multiplied by the probability of event B, given event A has already occurred. This is based on the principle of Conditional probability And can be written as P(B│A), and read as the “probability of B given A”. in general, conditional probability can be computed as

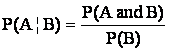. (4.4)

Then The Multiplication Rule for dependent events A and B can be written in (4.5)

P(A and B) = P(A) x P(B│A). (4.5)

The Rule of addition is used to find the probability of A Or B (AUB). This rule states that

1. If A and B are Mutually Exclusive events the probability of event A must be added to the probability of event B. The joint probability in this case is zero, i. e. P(A and B) = 0.

P(A or B) = P(A) + P(B). (4.6)

2. If A and B are Not mutually exclusive (both can occur at the same time) events the probability of event A must be added to the probability of event B and subtract the joint probability of events A and B. See formula (4.7).

P(A or B) = P(A) + P(B) – P(A and B). (4.7)

< Предыдущая		Следующая >