028. Other Measures of Dispersion
There are other ways the dispersion of a data set might be measured. These additional measures of dispersion, which often prove to be quite serviceable, are Quartiles, Deciles, and Percentiles.
Every data set has Three quartiles, which divide it into four equal parts. As seen in Figure 3.1, if the horizontal line can be thought of as a data set arranged in an ordered array, three quartiles can be identified, which together produce four separate parts or subsets of equal size in the data set.

Figure 3.1 - Three Quartiles Produce Four Equal Subsets
The First quartile (P25) is that value below which, at most, 25 percent of the observations fall, and above which the remaining 75 percent can be found. The Second quartile (P50) is right in the middle. One-half the observations are below it and one-half the observations are above it; in this sense, it is the same as the median. The Third quartile (P75) is that value below which, at most, 75 percent of the observations are located, and above which the remaining 25 percent can be found.
The determination of quartiles is often useful. Many graduate schools, for Example, will admit only those students in the top 25 percent (third quartile) of their applicants, etc.
Deciles separate a data set into 10 equal subsets, and percentiles produce 100 parts. The First decile (P10) is that observation below which, at most, 10 percent of the observations are found while the remaining 90 percent are located above it. The First percentile (P1) is that value below which no more than 1 percent of the observations are located, and the rest are above it, etc. Each data set has 9 deciles and 99 percentiles.
The Location Of the PTh percentile is found as
![]() , (3.18)
, (3.18)
Where Lp is the location in an ordered array of the desired percentile; N is the number of observations; P is the desired percentile.
Example 3.10. In Table 3.7 the observations for the number of shares for 50 stocks traded on the New York Stock Exchange are shown (in an ordered array). Assume that somebody wishes to calculate the 25th percentile, P25, for the stocks.
Table 3.7 – Numbers of Shares Traded on the NYSE (in 100’s)
|
3 |
10 |
19 |
27 |
34 |
38 |
48 |
56 |
67 |
74 |
|
4 |
12 |
20 |
29 |
34 |
39 |
48 |
59 |
67 |
74 |
|
7 |
14 |
21 |
31 |
36 |
43 |
52 |
62 |
69 |
76 |
|
9 |
15 |
25 |
31 |
37 |
45 |
53 |
63 |
72 |
79 |
|
10 |
17 |
27 |
34 |
38 |
47 |
56 |
64 |
73 |
80 |
First the location of the 25th percentile must be found in an ordered array.
![]() .
.
The resulting value of 12.75 tells that the 25th percentile is located 75 percent of the way between the 12th observation of 20 and the 13th observation of 21, or P25 = 20+(0.75)(21-20) = 20.75, or 2,075 shares since the data were originally expressed in hundreds of shares. Thus, 25 percent of the observations are below 20.75, and the remaining 75 percent are above 20.75.
The Interquartile range (IQR) is a unique measure of dispersion. The IQR is the difference between the first quartile and the third quartile. That is, P75 – P25. One-half of the observations lie within this range. It consists of the middle 50 percent of the observations in that it cuts off the lower 25 percent and the upper 25 percent of the data points.
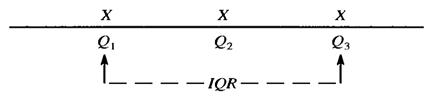
Figure 3.2 - The Interquartile Range
As a result, the IQR provides a measure of dispersion that is not heavily influenced by a few extreme observations.
| < Предыдущая | Следующая > |
|---|