4.3. Линейный регрессионный анализ и статистическое прогнозирование

Линейная регрессия является наиболее часто используемым видом регрессионно­го анализа. Ниже перечислены три основные задачи, решаемые в маркетинговых исследованиях при помощи линейного регрессионного анализа.

1. Определение того, какие частные параметры продукта оказывают влияние на общее впечатление потребителей от данного продукта. Установление направ­ления и силы данного влияния. Расчет, каким будет значение результирующе­го параметра при тех или иных значениях частных параметров. Например, тре­буется установить, как влияет возраст респондента и его среднемесячный доход на частоту покупок глазированных сырков.

2. Выявление того, какие частные характеристики продукта влияют на общее впе­чатление потребителей от данного продукта (построение схемы выбора продук­та потребителями). Установление соотношения между различными частными па­раметрами по силе и направлению влияния на общее впечатление. Например, имеются оценки респондентами двух характеристик мебели производителя X — цены и качества, — а также общая оценка мебели данного производителя. Требу­ется установить, какой из двух параметров является наиболее значимым для покупате­лей при выборе производителя мебели и в каком конкретном соотношении находится значимость для покупателей данных двух факторов (параметр Цена в х раз более значим для покупателей при выборе мебели, чем параметр Качество).

3. Графическое прогнозирование поведения одной переменной в зависимости от изменения другой (используется только для двух переменных). Как правило, целью проведения регрессионного анализа в данном случае является не столько расчет уравнения, сколько построение тренда (то есть аппроксимирующей кри­вой, графически показывающей зависимость между переменными). По полу­ченному уравнению можно предсказать, каким будет значение одной перемен­ной при изменении (увеличении или уменьшении) другой. Например, требуется установить характер зависимости между долей респондентов, осведомленных о раз­личных марках глазированных сырков, и долей респондентов, покупающих данные марки. Также требуется рассчитать, насколько возрастет доля покупателей сырков марки х при увеличении потребительской осведомленности на 10 % (в результате про­ведения рекламной кампании).

В зависимости от типа решаемой задачи выбирается вид линейного регрессионно­го анализа. В большинстве случаев (1 и 2) применяется множественная линейная регрессия, в которой исследуется влияние нескольких независимых переменных на одну зависимую. В случае 3 применима только простая линейная регрессия, в которой участвуют только одна независимая и одна зависимая переменные. Это связано с тем, что основным результатом анализа в случае 3 является линия трен­да, которая может быть логически интерпретирована только в двухмерном про­странстве. В общем случае результатом проведения регрессионного анализа явля­ется построение уравнения регрессии вида: у = а + Ь, х, + Ь2х2 + ... + Ь„хп, позволяющего рассчитать значение зависимой переменной при различных значе­ниях независимых переменных.

В табл. 4.6 представлены основные характеристики переменных, участвующих в анализе.

Таблица 4.6. Основные характеристики переменных, участвующих в линейном регрессионном анализе

Линейная регрессия
Зависимые переменные	Независимые переменные
Количество	Тип	Количество	Тип
Одна	Интервальная	Любое	Интервальная
	Порядковая		Порядковая
			Дихотомическая

В связи с тем что и множественная и простая регрессии строятся в SPSS одинако­вым способом, рассмотрим общий случай множественной линейной регрессии как наиболее полно раскрывающий суть описываемого статистического метода. Да­вайте рассмотрим, как построить линию тренда с целью статистического прогно­зирования.

Исходные данные:

В ходе опроса респондентов, летающих одним из трех классов (первым, бизнес - или эко­ном-классом), просили оценить по пятибалльной шкале — от 1 (очень плохо) до 5 (отлич­но) — следующие характеристики сервиса на борту самолетов авиакомпании X: комфор­табельность салона, работа бортпроводников, питание во время полета, цена билетов, спиртные напитки, дорожные наборы, аудиопрограммы, видеопрограммы и пресса. Также респондентам предлагалось поставить общую (итоговую) оценку обслуживания на борту самолетов данной авиакомпании.

Для каждого класса полета требуется:

1) Выявить наиболее значимые для респондентов параметры обслуживания на борту.

2) Установить, какое влияние оказывают оценки частных параметров обслуживания на борту на общее впечатление авиапассажиров от полета.

Откройте диалоговое окно Linear Regression при помощи меню Analyze ► Regres­sion ► Linear. Из левого списка выберите зависимую переменную для анализа. Это будет Общая оценка сервиса на борту. Поместите ее в область Dependent. Далее в ле­вом списке выберите независимые переменные для анализа: частные параметры сервиса на борту — и поместите их в область Independent(s).

Существует несколько методов проведения регрессионного анализа: enter, stepwise, forward и backward. He вдаваясь в статистические тонкости, проведем регрессион­ный анализ посредством пошагового метода backward как наиболее универсально­го и релевантного для всех примеров из маркетинговых исследований.

Так как задача анализа содержит требование провести регрессионный анализ в раз­резе трех классов полета, выберите в левом списке переменную, обозначающую класс (q5) и перенесите ее в область Selection Variable. Затем щелкните на кнопке Rule, чтобы задать конкретное значение данной переменной для регрессионного анализа. Следует отметить, что за одну итерацию можно построить регрессию толь­ко в разрезе какого-то одного класса полета. В дальнейшем следует повторить все этапы сначала по количеству классов (3), каждый раз выбирая следующий класс.

Если нет необходимости проводить регрессионный анализ в каком-либо разрезе, оставьте поле Selection Variable пустым.

Итак, на экране открылось диалоговое окно Set Rule, в котором вы должны указать, для какого именно класса полета вы хотите построить регрессионную модель. Выберите экономический класс, закодированный как 3 (рис. 4.26).

Рис. 4.26. Диалоговое окно Set Rule

 

В более сложных случаях, когда требуется построить регрессионную модель в раз­резе трех и более переменных, следует воспользоваться условным отбором дан­ных (см. раздел 1.5.1). Например, если кроме класса полета есть еще и необходи­мость раздельного построения регрессионной модели для респондентов (мужчин и женщин), необходимо перед открытием диалогового окна Linear Regression про­извести условный отбор анкет респондентов, являющихся мужчинами. Далее про­водится регрессионный анализ по описываемой схеме. Для построения регрес­сии для женщин следует повторить все этапы сначала: вначале выбрать только анкеты респондентов-женщин и затем уже для них построить регрессионную модель.

Щелкните на кнопке Continue в диалоговом окне Set Rule — вы вновь вернетесь к основному диалоговому окну Linear Regression. Последним шагом перед запуском процедуры построения регрессионной модели является выбор пункта Collinearity Diagnostics в диалоговом окне, появляющемся при щелчке на кнопке Statistics (рис. 4.27). Установление требования провести диагностику наличия коллинеар­ности между независимыми переменными позволяет избежать эффекта мульти-коллинеарности, при котором несколько независимых переменных могут иметь настолько сильную корреляцию, что в регрессионной модели обозначают, в прин­ципе, одно и то же (это неприемлемо).

Рис. 4.26. Диалоговое окно Set Rule

 

Теперь основное диалоговое окно Linear Regression примет вид, показанный на рис. 4.28. Щелчок на кнопке О К приведет к запуску процедуры построения линей­ной регрессии.

Рис. 4.28. Диалоговое окно Linear Regression

 

Рассмотрим основные элементы отчета о построении регрессионной модели (окно SPSS Viewer), содержащие наиболее значимые для исследователя данные. Не­обходимо отметить, что все таблицы, представленные в отчете Output, содержат несколько блоков, соответствующих количеству шагов SPSS при построении модели. На каждом шаге при используемом методе backward из полного списка независимых переменных, введенных в модель изначально, при помощи наимень­ших частных коэффициентов корреляции последовательно исключаются пере­менные — до тех пор, пока соответствующий коэффициент регрессии не оказы­вается незначимым (Sig > 0,05). В нашем примере таблицы состоят из трех блоков (регрессия строилась в три шага). При интерпретации результатов регрессион­ного анализа следует обращать внимание только на последний блок (в нашем случае 3).

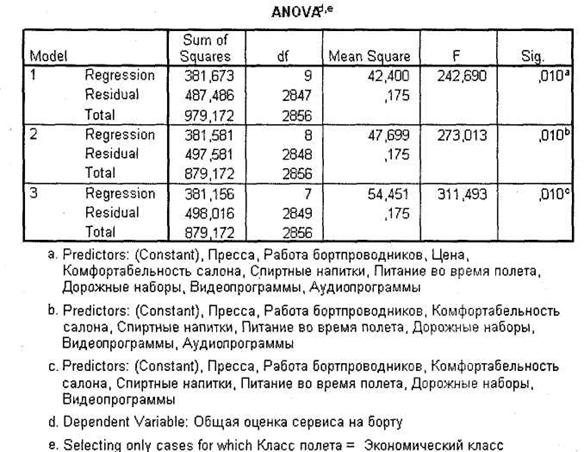
Первое, на что следует обратить внимание, — это таблица ANOVA (рис. 4.29). На третьем шаге статистическая значимость (столбец Sig) должна быть меньше или равна 0,05.

Затем следует рассмотреть таблицу Model Summary, содержащую важные сведения о построенной модели (рис. 4.30). Коэффициент детерминации R является харак­теристикой силы общей линейной связи между переменными в регрессионной модели. Он показывает, насколько хорошо выбранные независимые переменные способны определять поведение зависимой переменной. Чем выше коэффициент детерминации (изменяющийся в пределах от 0 до 1), тем лучше выбранные неза­висимые переменные подходят для определения поведения зависимой перемен­ной. Требования к коэффициенту R такие же, как к коэффициенту корреляции (см. табл. 4.4): в общем случае он должен превышать хотя бы 0,5. В нашем примере R = 0,66, что является приемлемым показателем.

Рис. 4.29. Таблица ANOVA

 

Также важной характеристикой регрессионной модели является коэффициент R2, показывающий, какая доля совокупной вариации в зависимой переменной описывается выбранным набором независимых переменных. Величина R2 из­меняется от 0 до 1. Как правило, данный показатель должен превышать 0,5 (чем он выше, тем показательнее построенная регрессионная модель). В нашем при­мере R2 =■ 0,43 — это значит, что регрессионной моделью описано только 43 % случаев (дисперсии в итоговой оценке полета). Таким образом, при интерпре­тации результатов регрессионного анализа следует постоянно иметь в виду су­щественное ограничение: построенная модель справедлива только для 43 % случаев.

Третьим практически значимым показателем, определяющим качество регресси­онной модели, является величина стандартной ошибки расчетов (столбец Std. Error of the Estimate). Данный показатель варьируется в пределах от 0 до 1. Чем он мень­ше, тем надежнее модель (в общем случае показатель должен быть меньше 0,5). В нашем примере ошибка составляет 0,42, что является завышенным, но в целом приемлемым результатом.

На основании таблиц AN OVA и Model Summary можно судить о практической пригод­ности построенной регрессионной модели. Учитывая, что AN OVA показывает весь­ма высокую значимость (менее 0,001), коэффициент детерминации превышает 0,6, а стандартная ошибка расчетов меньше 0,5, можно сделать вывод о том, что с уче­том ограничения модель описывает 43 % совокупной дисперсии, то есть построен­ная регрессионная модель является статистически значимой и практически при­емлемой.

Рис. 4.30. Таблица Model Summary

 

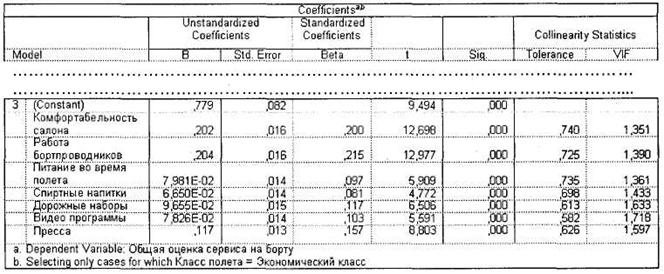
После того как мы констатировали приемлемый уровень качества регрессионной модели, можно приступать к интерпретации ее результатов. Основные практиче­ские результаты регрессии содержатся в таблице Coefficients (рис. 4.31). Под таб­лицей вы можете видеть, какая переменная была зависимой (общая оценка серви­са на борту) и для какого класса полета происходило построение регрессионной модели (эконом-класс). В таблице Coefficients практически значимыми являются четыре показателя: VIF, Beta, В и Std. Error. Рассмотрим последовательно, как их сле­дует интерпретировать.

Рис. 4.31. Таблица Coefficients

 

Прежде всего необходимо исключить возможность возникновения ситуации мультиколлинеарности (см. выше), при которой несколько переменных могут обозна­чать почти одно и то же. Для этого необходимо посмотреть на значение VIF возле каждой независимой переменной. Если величина данного показателя меньше 10 — значит, эффекта мультиколлинеарности не наблюдается и регрессионная модель приемлема для дальнейшей интерпретации. Чем выше этот показатель, тем более связаны между собой переменные. Если какая-либо переменная превышает значение в 10 VIF, следует пересчитать регрессию без этой независимой переменной. В данном примере автоматически уменьшится величина R2 и возрастет величина свободного члена (константы), однако, несмотря на это, новая регрессионная мо­дель будет более практически приемлема, чем первая.

В первом столбце таблицы Coefficients содержатся независимые переменные, со­ставляющие регрессионное уравнение (удовлетворяющие требованию статисти­ческой значимости). В нашем случае в регрессионную модель входят все частные характеристики сервиса на борту самолета, кроме аудиопрограмм. Исключенные переменные содержатся в таблице Excluded Variables (здесь не приводится). Итак, мы можем сделать первый вывод о том, что на общее впечатление авиапассажиров от полета оказывают влияние семь параметров: комфортабельность салона, работа бортпроводников, питание во время полета, спиртные напитки, дорожные наборы, видеопрограммы и пресса.

После того, как мы определили состав параметров, формирующих итоговое впе­чатление от полета, можно определить направление и силу влияния на него каж­дого частного параметра. Это позволяет сделать столбец Beta, содержащий стан­дартизированные - коэффициенты регрессии. Данные коэффициенты также дают возможность сравнить силу влияния параметров между собой. Знак (+ или -) пе­ред -коэффициентом показывает направление связи между независимой и зави­симой переменными. Положительные -коэффициенты свидетельствуют о том, что возрастание величины данного частного параметра увеличивает зависимую пере­менную (в нашем случае все независимые переменные ведут себя подобным обра­зом). Отрицательные коэффициенты означают, что при возрастании данного част­ного параметра общая оценка снижается. Как правило, при определении связи между оценками параметров это свидетельствует об ошибке и означает, например, что выборка слишком мала.

Например, если бы перед - коэффициентом параметра работы бортпроводников стоял знак -, его следовало бы интерпретировать следующим образом: чем хуже работают бортпроводники, тем лучше становится общее впечатление пассажиров от полета. Такая интерпретация является бессмысленной и не отражающей реаль­ного положения вещей, то есть ложной. В таком случае лучше пересчитать регрес­сию без данного параметра; тогда доля вариации в итоговой оценке, описываемой исключенным параметром, будет отнесена на счет константы (увеличивая ее). Соответственно уменьшится и процент совокупной дисперсии, описываемой рег­рессионной моделью (величина R2). Однако это позволит восстановить семанти­ческую релевантность.

Еще раз подчеркнем, что сделанное замечание справедливо для нашего случая (оценки параметров). Отрицательные - коэффициенты могут быть верными и от­ражать семантические реалии в других случаях. Например, когда уменьшение до­хода респондентов приводит к увеличению частоты покупок дешевых товаров. В таблице вы видите, что в наибольшей степени на общее впечатление пассажи­ров от полета влияют два параметра: работа бортпроводников и комфортабель­ность салона (- коэффициенты по 0,21). Напротив, в наименьшей степени форми­рование итоговой оценки сервиса на борту происходит за счет впечатления от обслуживания спиртными напитками (0,08). При этом два первых параметра ока­зывают почти в три раза более сильное влияние на итоговую оценку полета, чем

Спиртные напитки. На основании стандартизированных (3-коэффициентов регрес­сии можно построить рейтинг влияния частных параметров сервиса на борту на общее впечатление авиапассажиров от полета, разделив их на три группы по силе влияния:

■ наиболее значимые параметры;

■ параметры, имеющие среднюю значимость;

■ параметры, имеющие низкую значимость для респондентов (рис. 4.32).

В крайнем правом столбце содержатся - коэффициенты, умноженные на 100, — для облегчения сравнения параметров между собой.

Рис. 4.32. Рейтинг значимости параметров сервиса на борту

 

Данный рейтинг также можно интерпретировать и как рейтинг значимости для респондентов различных параметров сервиса на борту (в общем случае — схема выбора). Так, наиболее важными факторами являются первые два (1-2); среднюю значимость для пассажиров имеют следующие три параметра (3-5); относительно малое значение имеют последние два фактора (6-7).

Регрессионный анализ позволяет выявить истинные, глубинные мотивы респон­дентов при формировании общего впечатления о каком-либо продукте. Как пока­зывает практика, такого уровня приближения нельзя достичь обычными метода­ми — например, просто спросив респондентов: Какие факторы из нижеперечисленных оказывают наибольшее влияние на Ваше общее впечатление от полета самолетами нашей авиакомпании?. Кроме того, регрессионный анализ позволяет достаточно точно оце­нить, насколько один параметр более-менее значим для респондентов, чем другой, и на этом основании классифицировать параметры на критические, имеющие сред­нюю значимость и малозначимые.

Столбец В таблицы Coefficients содержит коэффициенты регрессии (нестандарти-зированные). Они служат для формирования собственно регрессионного уравне­ния, по которому можно рассчитать величину зависимой переменной при разных значениях независимых.

Особая строка Constant содержит важную информацию о полученной регрессион­ной модели: значение зависимой переменной при нулевых значениях независимых переменных. Чем выше значение константы, тем хуже подходит выбранный перечень независимых переменных для описания поведения зависимой перемен­ной. В общем случае считается, что константа не должна быть наибольшим коэффи­циентом в регрессионном уравнении (коэффициент хотя бы при одной переменой должен быть больше константы). Однако в практике маркетинговых исследова­ний часто свободный член оказывается больше всех коэффициентов вместе взя­тых. Это связано в основном с относительно малыми размерами выборок, с кото­рыми приходится работать маркетологам, а также с неаккуратным заполнением анкет (некоторые респонденты могут не поставить оценку каким-либо парамет­рам). В нашем случае величина константы меньше 1, что является весьма хоро­шим результатом.

Итак, в результате построения регрессионной модели можно сформировать сле­дующее регрессионное уравнение:

СБ = 0,78 + 0,20К + 0.20Б + 0,08ПП + 0.07С + 0Д0Н + 0,08В + 0Д2П, где

■ СБ — общая оценка сервиса на борту;

■ К — комфортабельность салона;

■ Б — работа бортпроводников;

■ ПП — питание во время полета;

■ С — спиртные напитки;

■ Н — дорожные наборы;

■ В — видеопрограмма;

■ П — пресса.

Последний показатель, на который целесообразно обращать внимание при интер­претации результатов регрессионного анализа, — это стандартная ошибка, рассчи­тываемая для каждого коэффициента в регрессионном уравнении (столбец Std. Error). При 95%-ном доверительном уровне каждый коэффициент может отклоняться от величины В на ±2 х Std. Error. Это означает, что, например, коэффициент при пара­метре Комфортабельность салона (равный 0,202) в 95 % случаев может отклоняться от данного значения на ±2 х 0,016 или на ±0,032. Минимальное значение коэффициен­та будет равно 0,202 - 0,032 = 0,17; а максимальное - 0,202 + 0,032 = 0,234. Таким образом, в 95 % случаев коэффициент при параметре «комфортабельность салона» варьируется в пределах от 0,17 до 0,234 (при среднем значении 0,202). На этом интерпретация результатов регрессионного анализа может считаться за­вершенной. В нашем случае следует повторить все шаги еще раз: сначала для биз­нес -, потом для эконом-класса.

Теперь давайте рассмотрим другой случай, когда необходимо графически пред­ставить зависимость между двумя переменными (одной зависимой и одной неза­висимой) при помощи регрессионного анализа. Например, если мы примем итого­вую оценку полета авиакомпанией X в 2001 г. за зависимую переменную S,, а тот же показатель в 2000 г. — за независимую переменную So, то для построения урав­нения тренда (или регрессионного уравнения) нужно будет определить парамет­ры соотношения S, = а + b x So. Построив данное уравнение, также можно построить регрессионную прямую и, зная исходную итоговую оценку полета, спрогнози­ровать величину данного параметра на следующий год.

Эту операцию следует начать с построения регрессионного уравнения. Для этого повторите все вышеописанные шаги для двух переменных: зависимой Итоговая оценка 2001 и независимой Итоговая оценка 2000. Вы получите коэффициенты, при помощи которых можно в дальнейшем строить линию тренда (как в SPSS, так и любыми другими средствами). В нашем случае полученное регрессионное уравне­ние имеет вид: S{ = 0,18 + 0,81 х So. Теперь построим уравнение линии тренда в SPSS.

Диалоговое окно Linear Regression имеет встроенное средство для построения гра­фиков — кнопку Plots. Однако это средство, к сожалению, не позволяет на одном графике построить две переменные: S, и So - Для того чтобы построить тренд, необ­ходимо использовать меню Graphs ► Scatter. На экране появится диалоговое окно Scatterplot (рис. 4.32), которое служит для выбора типа диаграммы. Выберите вид Simple. Максимально возможное число независимых переменных, которое можно изобразить графически, — 2. Поэтому при необходимости графического построе­ния зависимости одной переменной (зависимой) от двух независимых (например, если бы в нашем распоряжении были данные не по двум, а по трем годам), в окне Scatterplot следует выбрать 3-D. Схема построения трехмерной диаграммы рассея­ния не имеет существенных отличий от описываемого способа построения двух­мерной диаграммы.

Рис. 4.33. Диалоговое окно Scatterplot

После щелчка на кнопке Define на экране появится новое диалоговое окно, пред­ставленное на рис. 4.34. Поместите в поле Y Axis зависимую переменную (Итоговая оценка 2001), а в поле X Axis — независимую (Итоговая оценка 2000). Щелкните на кнопке 0 К, что приведет к построению диаграммы рассеяния.

Для того чтобы построить линию тренда, дважды щелкните мышью на получен­ной диаграмме; откроется окно SPSS Chart Editor. В этом окне выберите пункт меню Chart ► Options; далее пункт Total в области Fit Line; щелкните на кнопке Fit Options. Откроется диалоговое окно Fit Line, выберите в нем тип аппроксимирующей ли­нии (в нашем случае Linear regression) и пункт Display R-square in legend. После за­крытия окна SPSS Chart Editor в окне SPSS Viewer появится линейный тренд, ап­проксимирующий наши наблюдения по методу наименьших квадратов. Также на диаграмме будет отражаться величина R2, которая, как было сказано выше, обо­значает долю совокупной вариации, описываемой данной моделью (рис. 4.35). В на­шем примере она равна 53 %.

С линейным регрессионным анализом связано множество интегральных показателей, рассчитываемых на основании коэффициентов регрессии (чаще всего стандартизированных). В качестве примера приведем расчет коэффициента потребительской привлекательности продукта/марки (Consumer Attractiveness), или коэффициента СА.

Рис. 4.34. Диалоговое окно Simple Scatterplot

Рис. 4.35. Диаграмма Scatterplot с построенной линией тренда

Этот коэффициент вводится в маркетинговых исследованиях для удобства сравне­ния привлекательности для респондентов анализируемых продуктов/марок. В анке­те должны присутствовать вопросы типа Оцените представленные параметры продукта/ марки X, в которых респондентам предлагается дать свои оценки частным параметрам продукта или марки X, скажем, по пятибалльной шкале (от 1 — очень плохо до 5 — отлично). В конце списка оцениваемых частных параметров респонденты должны поставить итоговую оценку продукту/марке X. При анализе полученных в ходе опро­са ответов респондентов на основании оценок респондентов формируются:

■ матрица средневзвешенных оценок по параметрам продукта/марки;

■ список стандартизированных - коэффициентов регрессии (оценка влияния частных параметров продукта/марки X на его/ее общую оценку).

Далее коэффициент СА рассчитывается по следующей формуле:

Где n — число параметров, формирующих итоговую оценку продукта или марки:

- — значимость для респондентов параметра с индексом i (стандартизированный -коэффициент регрессии, оценивающей влияние частных параметров на общую оценку продукта/марки, подробнее см. выше); — уровень средневзвешенной оценки продукта/марки по параметру с индексом i (при наличии пятибалльной шкалы):

= 2 при высоком уровне оценки (средневзвешенный балл ≥ 4,5)

= 1 при среднем уровне оценки (средневзвешенный балл ≥4,0 и < 4,5)

= -1 при низком уровне оценки (средневзвешенный балл ≥3,0 и < 4,0)

= -2 при неудовлетворительной оценке (средневзвешенный балл < 3,0)

Рассчитанный для каждого конкурирующего продукта/марки коэффициент СА показывает его/ее относительную позицию в структуре потребительских предпоч­тений. Данный интегральный показатель учитывает уровень оценок по каждому параметру, скорректированный на их значимость. При этом он может изменяться в пределах от -1 (наихудшая относительная позиция среди всех рассматриваемых продуктов/марок) до 1 (наилучшее положение); 0 означает, что данный продукт/ марка ничем особенным не выделяется в глазах респондентов.

Итогом расчета коэффициента СА является рейтинг конкурентов по данному по­казателю. На основании рейтинга можно сделать важные выводы относительно лидерства и аутсайдерства конкретных продуктов/марок на потребительском рынке.

Мы завершаем рассмотрение ассоциативного анализа. Данная группа статисти­ческих методов применяется в отечественных компаниях в настоящее время дос­таточно широко (особенно это касается перекрестных распределений). Вместе с тем хотелось бы подчеркнуть, что только лишь перекрестными распределениями ассоциативные методы не ограничиваются. Для проведения действительно глубо­кого анализа следует расширить спектр применяемых методик за счет методов, описанных в настоящей главе.

< Предыдущая		Следующая >