3.2.3. Многомерный дисперсионный анализ

Многомерный дисперсионный анализ является дальнейшим расширением од­номерного дисперсионного анализа (после рассмотренного в разделе 3.2.2 ANOVARM), предназначенным для одновременного анализа сразу нескольких зависимых и независимых переменных. Процесс проведения многомерного ана­лиза аналогичен рассмотренному выше обычному одномерному дисперсионному анализу, за исключением того, что в данном случае в область для зависимых пере­менных можно поместить сразу несколько переменных, а при интерпретации при­ходится анализировать сразу несколько различий (во всех зависимых перемен­ных).

Давайте рассмотрим процесс проведения многомерного дисперсионного анализа на примере, аналогичном приведённому в разделе 3.2.1 для обычного одномерного дисперсионного анализа, — но в качестве зависимых переменных мы будем рас­сматривать не только кратность покупок глазированных сырков, но и частоту по­купок. В качестве независимых переменных мы возьмем также две переменные: возраст респондентов и количество членов их семей.

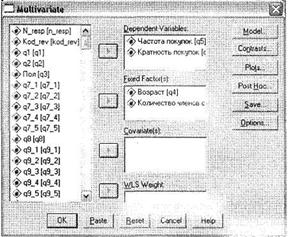
Откройте диалоговое окно Multivariate при помощи меню Analyze ► General Linear Model ► Multivariate. Как вы видите на рис. 3.31, оно аналогично окну Univariate. По­местите две зависимые переменные: q5 (Частота покупок) и q6 (Кратность покупок) в область для зависимых переменных Dependent Variables, а переменные q4 (Возраст) и q72 (Количество членов семьи) — в область для независимых переменных Fixed Factor(s). После этого так же, как для одномерного дисперсионного анализа в окне Post Hoc, задайте вывод тестов Scheffe и Tumhale для обеих независимых перемен­ных, а в окне Options отметьте параметр Homogeneity Tests. После этого можно на­чать расчеты, щелкнув на кнопке ОК.

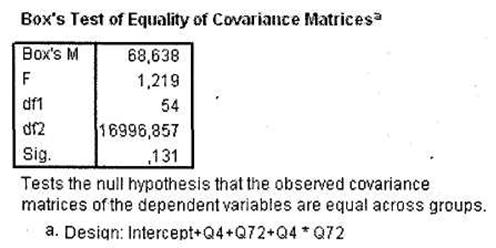
В окне SPSS Viewer появятся результаты многомерного дисперсионного анализа. Первой таблицей, которая должна привлечь ваше внимание, является Box's Test of Equality of Covariance Matrices, представленная на рис. 3.32. В отличие от одномерно­го дисперсионного анализа с повторяющимися измерениями, здесь тест Box дол­жен быть незначимым (как в нашем случае, Sig. = 0,131), так как неравенство дис­персий исследуемых зависимых переменных в многомерном анализе не является положительным фактом. И напротив, равенство дисперсий зависимых перемен­ных является одним из основных условий проведения многомерного дисперсион­ного анализа1.

Таблица Multivariate Tests позволяет сделать выводы относительно влияния не­зависимых переменных в отдельности, а также их взаимодействий на зависимые переменные в целом. Поскольку с практической точки зрения влияние не несет никакой смысловой нагрузки, данная таблица обычно не рассматрива­ется.

Рис. 3.31. Диалоговое окно Multivariate

Рис. 3.32. Таблица Box's Test of Equality of Covariance Matrices

Следующей важной таблицей является тест Levene на равенство дисперсий зави­симых переменных. Как мы помним из описания одномерного дисперсионного анализа, от факта равенства/неравенства дисперсий в дальнейшем зависит выбор конкретного апостериорного теста: Scheffe или Tumhale. Как вы видите на рис. 3.33, в нашем случае дисперсии равны у обеих зависимых переменных, поэтому далее мы будем опираться на результаты теста Scheffe.

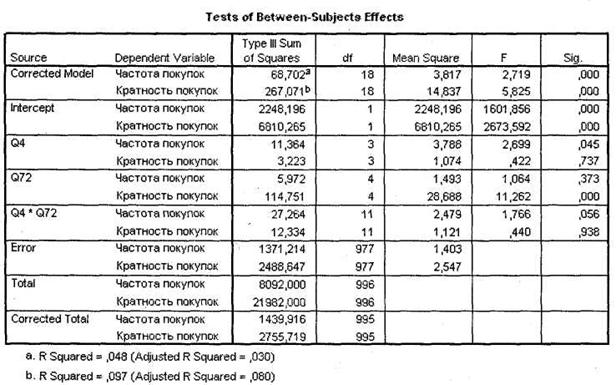
Таблица Tests of Between-Subjects Effects (рис. 3.34) позволяет установить, как каждый эффект влияет на каждую зависимую переменную в отдельности. В от­личие от таблицы Multivariate Tests, рассматриваемая таблица позволяет выяс­нить, на какую конкретно зависимую переменную влияет та или иная незави­симая переменная и их комбинации. В нашем случае мы видим, что частота покупок определяет различия между категориями переменной q4 Возраст (Sig. = 0,045), а кратность покупок — в категориях переменной q72 Количество членов семьи (Sig. < 0,001).

Рис. 3.33. Таблица Levene's Test of Equality of Error Variances

Рис. 3.34. Таблица Tests of Between-Subiects Effects

 

И наконец, последнее, что важно при практической интерпретации результатов многомерного дисперсионного анализа: какие группы каждой из рассматриваемых независимых переменных различаются на основании средних значений зависи­мых переменных. Это позволяют определить апостериорные тесты (в нашем слу­чае Scheffe). Они рассчитываются для каждой комбинации зависимая перемен­ная/ независимая переменная для всех значений индексов i. Эти таблицы по своему виду аналогичны рассмотренным в предыдущих разделах, посвященных диспер­сионному анализу.

Мы не приводим полностью результаты апостериорных тестов из-за их большого объема.

На рис. 3.35 представлены результирующие таблицы Homogenous Subsets, по ко­торым можно сделать выводы относительно различий между отдельными кате­гориями независимых переменных на основании обеих рассматриваемых зави­симых переменных. Также в этих таблицах вы видите однородные кластеры респондентов, различающиеся частотой и кратностью покупок глазированных сырков.

Рис. 3.35. Таблицы Homogeneous Subsets для переменных Возраст и Количество членов семьи

Итак, в данной главе мы рассмотрели статистические методы, применяемые для анализа различий между целевыми группами респондентов. Несмотря на то что данные методы (особенно обобщенная линейная модель) достаточно сложны для изучения, их применение позволяет поднять аналитическую работу на существен­но более высокий уровень.

< Предыдущая		Следующая >