2.1. Линейные распределения для одновариантных вопросов

Одновариантные вопросы являются основным ресурсом анализа при помощи SPSS. Практически все функции, реализованные в данном программном пакете, пред­назначены для работы только с одновариантными переменными. Анализ многова­риантных переменных производится методом выделения каждого варианта отве­та в отдельную одновариантную переменную и последующей работы уже с набором одновариантных переменных. Существуют табличные и графические способы по­строения линейных распределений по одновариантным вопросам. Ниже представ­лен способ, наиболее распространенный в маркетинговых исследованиях. Рассмотрим линейное распределение респондентов по возрастному признаку. Для этого предположим, что у нас есть файл данных, содержащий одновариантную переменную q4 (Возраст), имеющую порядковую шкалу, с четырьмя возможными вариантами ответа:

1. от 16 до 18 лет;

2. от 19 до 35 лет;

3. от 36 до 60 лет;

4. старше 60 лет.

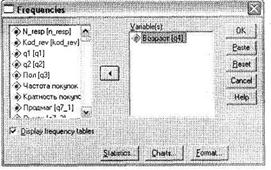
Вызов диалогового окна для построения линейных распределений (также называе­мых частотами) осуществляется при помощи меню Analyze ► Descriptive Statis­tics ► Frequencies (рис. 2.1). В открывшемся окне в левом списке содержатся все доступные переменные, по которым можно построить линейные распределения. При помощи мыши перетащите нужные одновариантные переменные в правый список (в нашем случае — q4). При этом для анализа можно указать сразу несколь­ко переменных.

Рис. 2.1. Диалоговое окно Frequencies с Выбранной для анализа переменной Возраст

В диалоговом окне Statistics, вызываемом при помощи одноименной кнопки, мож­но указать, какие описательные статистики, кроме относительных и абсолютных значений, необходимо рассчитать (рис. 2.2). Например, рассчитаем моду (наибо­лее часто встречающееся значение), выбрав соответствующий параметр. Кроме этой статистики, SPSS позволяет рассчитать другие полезные величины:

■ среднее арифметическое для интервальных переменных (Mean);

■ минимальное и максимальное значения (Minimum и Maximum), — а также разбить значения переменной на квартили или другие процентили (об­ласть PercentiLe Values) и т. д.

Однако большинство представленных в этом диалоговом окне статистик подхо­дит только для переменных, имеющих интервальный тип шкалы. Закрыв диалого­вое окно Statistics посредством щелчка на кнопке Continue, вы вновь попадете в ос-, новное окно Frequencies.

Рис. 2.2. Диалоговое окно Statistics

Необходимо сказать несколько слов относительно основных описательных ста­тистик, показанных на рис. 2.2. Пожалуй, наиболее популярными характерис­тиками, используемыми для описания переменных, являются показатели груп­пы Central Tendency (центральная тенденция): среднее арифметическое (Mean); медиана, или половина значений отрезка (Median); мода, или наиболее часто встречающееся значение (Mode); а также сумма (Sum). Имейте в виду, что дан­ные показатели применяются неодинаково к переменным с различным типом шкалы (табл. 2.3).

Таблица 2.3. Наиболее релевантные показатели центральной тенденции для переменных с различным типом шкалы

Тип шкалы	Наиболее релевантная характеристика	Другие релевантные характеристики
Интервальная	Среднее арифметическое	Средневзвешенное, мода
Порядковая	Средневзвешенное	Мода
Номинальная	Мода	-

Из представленной таблицы видно, что наиболее релевантной описательной ста­тистикой, характеризующей переменные с интервальной шкалой, является сред­нее арифметическое (Mean). Для переменных с порядковой шкалой данный пока­затель неприменим, так как он рассчитывается исходя из значений переменной (кодов вариантов ответа), а не самих значений интервалов.

Например, если рассчитать простое среднее по переменной Возраст (в которой воз­растные группы закодированы цифрами от 1 до 4), получится 250,5 (см. рис. 2.6). Данное значение не несет в себе практически значимой нагрузки. Если же мы вме­сто этого рассчитаем средневзвешенное значение данной переменной по нижепри­веденной формуле, мы получим реальный средний возраст респондентов: 43 года (43 - (408 × 48 + 321 × 27 + 207 ×68 + 66 × 17) / (408 + 321 + 207 + 66)).

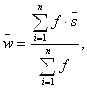
Где — средневзвешенное значение; n — количество интервалов (вариантов от­вета) в порядковой переменной; — частота появления i-го варианта ответа; — среднее арифметическое значение i-ro интервала.

Средняя тенденция переменных с номинальной шкалой не может быть оценена никак, кроме моды, — то есть для таких переменных можно определить только наи­более многочисленную группу. Например, по переменной Пол можно сказать, что в данном случае мужчины составляют три четверти всей выборочной совокупно­сти респондентов.

В табл. 2.2 также видно, что интервальные переменные — наиболее гибкие относи­тельно применения показателей центральной тенденции. Для них можно рассчи­тать все три рассматриваемые статистики: среднее арифметическое, средневзве­шенное и моду. Порядковые переменные находятся на втором месте: с ними могут использоваться только средневзвешенное и мода. И наконец, номинальные пере­менные являются наименее гибкими: к ним может эффективно применяться толь­ко мода.

Теперь мы вновь возвращаемся к диалоговому окну Frequencies. Кнопка Charts вы­зывает одноименное диалоговое окно, которое позволяет помимо таблиц вывести диаграммы по выбранным переменным (рис. 2.3). По умолчанию SPSS не выводит диаграмм. Давайте построим круговую диаграмму (сектограмму), выбрав параметр Pie charts и указав в области Chart Values на необходимость отобразить на диаграмме не абсолютные (установлено по умолчанию), а относительные значения (Percen­tages). Выполнив это, закройте диалоговое окно Charts.

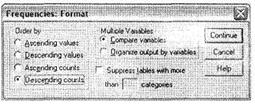
С помощью кнопки Format в главном диалоговом окне линейных распределений Frequencies можно указать, каким способом следует сортировать результаты в час­тотных таблицах (рис. 2.4). Это можно сделать, выбрав соответствующий пара­метр в области Order by. При этом возможной альтернативой будет сортировка ко­дов вариантов ответа (в нашем случае — кодировок возрастных групп):

■ по возрастанию: от 1 (16-18 лет) до 4 (старше 60 лет);

■ по убыванию: от 4 до 1;

■ по количеству респондентов, выбравших каждый из рассматриваемых вариан­тов ответа (в нашем случае — по численности четырех рассматриваемых возра­стных групп).

Рис. 2.3. Диалоговое окно Charts

Для иллюстрации нашего примера выберем сортировку по численности возраст­ных групп по убыванию Descending counts и закроем диалоговое окно Format, щелк­нув на кнопке Continue.

Рис. 2.4. Диалоговое окно Format

После щелчка на кнопке ОК в главном диалоговом окне Frequencies откроется окно SPSS Viewer, в котором будут представлены частотные таблицы, а также другая ин­формация, указанная нами на подготовительном этапе.

В таблице Statistics (рис. 2.5) отражаются общие параметры линейного распреде­ления. Здесь представлены:

■ количество респондентов, ответивших на вопрос Возраст (строка Valid), — 1002 че­ловека;

■ количество анкет, в которых на данный вопрос не было получено ответа (стро­ка Missing), — 1 человек;

■ мода (строка Mode), то есть наиболее многочисленная возрастная группа рес­пондентов (в нашем случае вариант 3: лица от 36 до 60 лет).

Следующая таблица, озаглавленная меткой анализируемой переменной (Возраст), отражает количество респондентов, которые указали тот или иной вариант ответа (столбец 2, Frequency), отсортированный по убыванию (рис. 2.6). Также в этой таб­лице представлен процент лиц, указавших данные варианты ответа от общего чис­ла респондентов (столбец 3, Percent) и от числа ответивших на анализируемый во­прос Возраст (столбец 4, Valid Percent). Последний столбец 5 (Cumulative Percent)

Отражает кумулятивные проценты (то есть вклад каждого варианта ответа в об­щую сумму). Так же как и в таблице Statistics, здесь указано общее количество от­ветивших (строка Valid Total) и не ответивших (строка Missing System) на данный вопрос, а также общее количество респондентов (строка Total, в нашем случае 1003).

Statistics

N	Valid	1002
	Missing	1
Mode		3

Рис. 2.5. Таблица Statistics

Возраст

	Frequency	Percent	Valid Percent	Cumulative Percent
Valid	36-60 лет	408	40,7	40,7	40,7
	19-35 лет	321	32,0	32,0	72,8
	Старше 60 лет	207	20,6	20,7	93,4
	16-18 лет	66	6,6	6,6	100,0
	Total	1002	99,9	100,0
Missing	System	1	,1
Total	Рис. 2.6. Таблица Возраст	1003	100,0

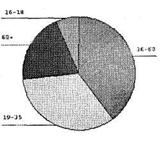
На подготовительном этапе анализа мы указали на необходимость построения сектограммы по рассматриваемой переменной. Она представлена в результатах ли­нейных распределений после таблицы Возраст (рис. 2.7). Несмотря на то, что мы прямо указали SPSS вывести на диаграмме проценты каждой возрастной группы, программа проигнорировала это указание: в построенной сектограмме указаны только названия категорий.

Рис. 2.7. Диаграмма Возраст

К сожалению, графическая подсистема SPSS весьма слаба и не выдерживает срав­нения со средствами Microsoft Office. Поэтому рекомендуем пользоваться ею, только когда это действительно оправдано (например, в дисперсионном анализе). Во всех остальных случаях предпочтительнее копировать выводимые таблицы в Mi­crosoft Excel и уже там строить по полученным данным диаграммы.

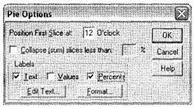
В рассматриваемом случае, чтобы исправить ситуацию и вывести проценты, дваж­ды щелкните мышью по диаграмме Возраст в окне SPSS Viewer. Откроется специаль­ное окно SPSS Chart Editor, предназначенное для редактирования простых диаграмм (simple charts)1. В нем выберите меню Chart ► Options. Откроется диалоговое окно Pie Options, в котором следует указать параметр Percents в области Labels (рис. 2.8). Далее щелкните на кнопке ОК и закройте окно SPSS Chart Editor. В окне SPSS Viewer к построенной диаграмме будут добавлены проценты каждой возрастной группы.

Рис. 2.8. Диалоговое окно Pie Options

Существует еще один способ построения диаграмм по линейным распределениям. Он применяется в случае, если вы уже построили частотную таблицу, но не указа­ли на подготовительном этапе на необходимость вывести диаграмму. В такой си­туации следует дважды щелкнуть мышью на данной таблице в окне SPSS Viewer, a затем выделить тот ее столбец, по которому необходимо построить диаграмму. Например, выделите столбец Valid Percent (значения во всех четырех строках, обо­значающих варианты ответа на вопрос Возраст). Затем щелкните правой кнопкой мыши и в открывшемся контекстном меню выберите пункт Create Graph ► Pie для построения сектограммы по долям каждой возрастной группы. В результате после частотной таблицы будет выведена соответствующая круговая диаграмма.

В разделе 1.2 было показано, как рассчитывается статистическая ошибка для ве­личин, выраженных в процентах. Теперь, после того как мы изучили линейные распределения и основные описательные статистики, можно рассмотреть форму­лу для расчета статистической ошибки значений, выраженных в абсолютных ве­личинах (например, средние значения). Напомним, что статистическая ошибка для данной категории величин рассчитывается для каждой из них в отдельности.

В качестве примера рассмотрим линейное распределение оценок на вопрос Оцени­те, пожалуйста, качество сухих строительных смесей марки X по пятибалльной шкале: от 1 (очень плохо) до 5 (отлично). При этом в диалоговом окне Statistics (см. рис. 2.2) не­обходимо выбрать параметры: Mean (среднее арифметическое) и Variance (диспер­сия). После окончания расчетов в окне SPSS Viewer будет выведена следующая таблица (рис. 2.9).

Statistics

N	Valid	6762
	Missing	1406
Mean		3,89
Variance		,634

Рис. 2.9. Таблица Statistics

Формула для расчета статистической ошибки величин, выраженных в абсолютных показателях, имеет следующий вид:

Где z — статистическая константа для выбранного доверительного уровня (см. табл. 1.1); — дисперсия (строка Variance в таблице Statistics на рис. 2.9); n — раз­мер выборки для данного вопроса (строка Valid в таблице Statistics на рис. 2.9).

Таким образом, для нашего случая и стандартного для маркетинговых иссле­дований доверительного уровня в 95 % статистическая ошибка выборки будет равна:

То есть средняя оценка качества ССС варьируется в пределах от 3,87 балла (3,89 --0,02) до 3,91 (3,89+ 0,02).

< Предыдущая		Следующая >