31.1. Интерполяционный многочлен Лагранжа

Интерполяционным многочленом Лагранжа называется многочлен

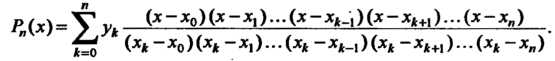(31.1)

Этот многочлен удовлетворяет условиям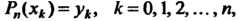Где—

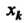Узлы (или полюсы) интерполяции,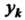— заданные числа.

Интерполяционной формулой Лагранжа называется формула

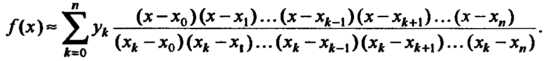(31.2)

Формулы (31.1) и (31.2) можно записать так:

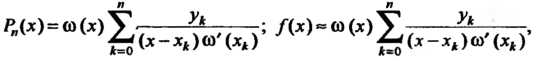
Где

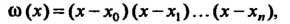(31.3)

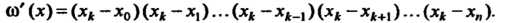
Производя интерполирование функции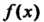По формуле Лагранжа (31.2), заменяют эту функцию полиномом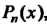, совпадающим с ней в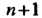Данных точках отрезка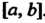, В остальных точках этого отрезка разность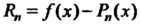

Отлична от нуля и представляет собой погрешность метода. Эта разность, называемая остаточным членом интерполяции, определяется формулой

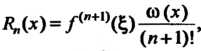
В которой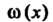Выражается равенством (31.3),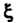- точка промежутка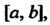

Зависящая от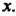

Пример 31.1. Найти интерполяционный многочлен Лагранжа, который в точках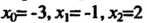Принимает соответственно значения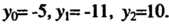

При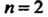Формула (31.1) имеет вид

Подставляя в эту формулу заданные значения, находим 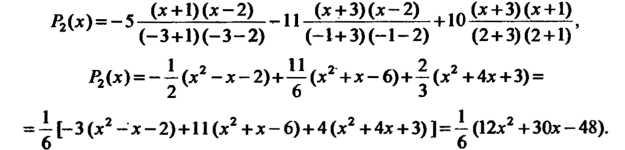 Итак,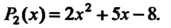

Пример 31.2. Найти интерполяционный многочлен Лагранжа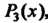, для которого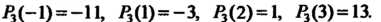

В данном случае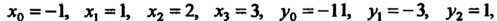

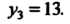При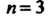Формула (31.1) принимает вид

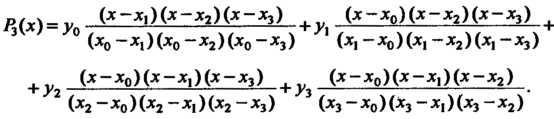
Подставляя в эту формулу данные значения, получаем 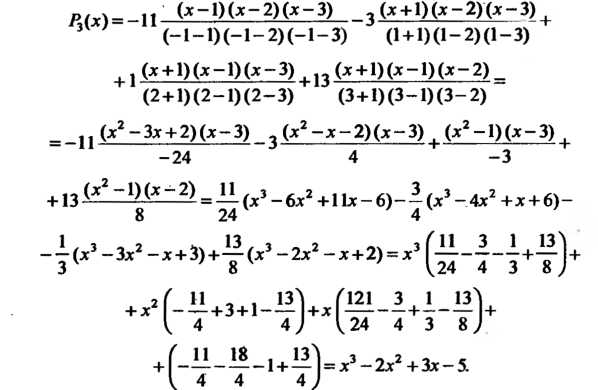 Следовательно,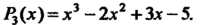

Термин «интерполяция» впервые употребил Д. Валлис (1656) при составлении астрономических и математических таблиц.

< Предыдущая		Следующая >