15.06. Исследование функций и построение их графиков
Под исследованием функций понимают изучение их изменения в зависимости от изменения аргумента. На основании исследования функции строят ее график, предварительно изображая характерные точки.
Исследование функций и построение их графиков можно проводить по следующей схеме.
1. Найти область определения функции, ее точки разрыва.
2. Изучить изменение функции при стремлении аргумента к концам промежутков области определения.
3. Найти точки экстремумов, промежутки возрастания и убывания функции.
4. Вычислить значения экстремумов, построил, соответствующие точки.
5. Определить промежутки выпуклости и вогнутости графика, найти точки перегиба.
6. Найти точки пересечения графика с координатными осями.
7. Найти асимптоты графика функции.
Порядок исследования иногда целесообразно выбирать исходя из конкретных особенностей данной функции.
Если рассматриваемая функция четная или нечетная, то ее достаточно исследовать при положительных значениях аргумента из области ее определения и принять во внимание, что график четной функции симметричен относительно, оси ординат, а график нечетной - относительно начала координат.
Отметим также, что графики взаимно обратных функций симметричны относительно прямой, на которой лежит биссектриса первого координатного угла.
Пример 15.12. Исследовать функцию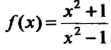 И построить ее график.
И построить ее график.
1. Функция не определена лишь при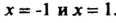 . Следовательно, область определения состоит из трех интервалов:
. Следовательно, область определения состоит из трех интервалов: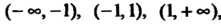 , два из которых являются бесконечными.
, два из которых являются бесконечными.
2. При стремлении аргумента к концам промежутков области определения соответственно получаем
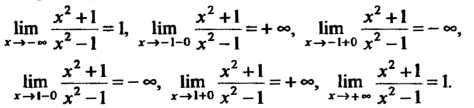
3. Находим производные данной функции:
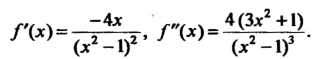
Поскольку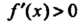 При
При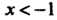 И
И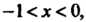 То функция возрастает в интер
То функция возрастает в интер
Валах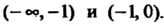 Так как
Так как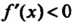 При
При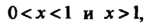 То функция
То функция
Убывает в интервалах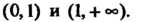
Поскольку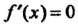 При
При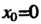 И
И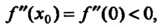 То
То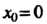 - точка максимума.
- точка максимума.
Других критических точек нет, ибо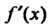 Не определена только при
Не определена только при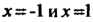 ,но
,но
В этих точках не определена и сама функция.
4. Вычисляем значение максимума функции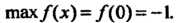
5. Поскольку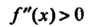 При
При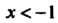 И
И 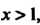 То график функции является выпуклым вниз в интервалах
То график функции является выпуклым вниз в интервалах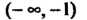 И
И
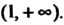 Так как
Так как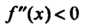 При
При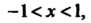
То график функции является выпуклым вверх в интервале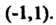
Точек перегиба график данной функции не имеет, ибо вторая производная в нуль нигде не обращается и не определена в тех же точках, в которых не определена и сама функция.
6. График функции не пересекает ось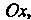 Так как уравнение
Так как уравнение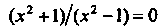
Не имеет действительных корней. Если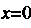 1 (уравнение оси
1 (уравнение оси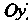 ), то
), то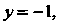 В точке
В точке
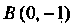 График пересекает ось Оу.
График пересекает ось Оу.
7. Из п. 2 следует, что график функции имеет две вертикальные асимптоты
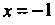 И
И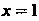 И горизонтальную асимптоту
И горизонтальную асимптоту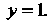 Последнее вытекает также из
Последнее вытекает также из
Того, что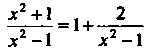 И
И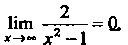
Заметив еще, что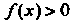 При
При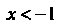 И
И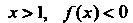 При
При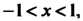 Стро
Стро
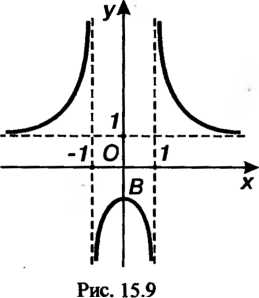
Им график функции (рис. 1S.9).
| < Предыдущая | Следующая > |
|---|