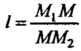01.01. Координаты на прямой

На прямой зафиксируем одно из двух определяемых ею направлений и назовем его положительным, другое - отрицательным. Прямую, на которой указано положительное направление, называют осью.

Отрезок, ограниченный точками А и В, называют направленным отрезком или вектором, если указано, какая из данных точек является началом, какая — концом. Направленный отрезок с началом в точке А и концом в точке В обозначают АВ.

Величиной направленного отрезка АВ некоторой оси называют его длину, взятую со знаком плюс, когда направление этого отрезка совпадает с положительным направлением данной оси, и со знаком минус, когда оно совпадает с отрицательным направлением оси. Величину направленного отрезка АВ обозначают АВ.

Координатной осью называют прямую, на которой зафиксированы начало отсчета, положительное направление и выбран масштаб для измерения длин.

Координатой точки М координатной оси (рис. 1.1) называют величину ОМ направленного отрезка ОМ, где О - начало координат. Если обозначить координату точки М через х, то по определению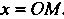

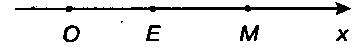
Рис. 1.1

Запись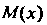Означает, что точка М имеет координату х.

Если даны две точкиИТо величина направленного отрезка

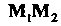Вычисляется по формуле

(1.1)

А расстояние между ними - по формуле

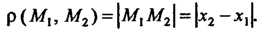
Простым отношением трех различных точек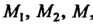, лежащих на одной

Прямой и взятых в указанном порядке, называют число

(13)

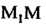ГдеИ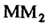- величины направленных отрезковИ

Если точка М принадлежит отрезку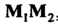, простое отношение положительно

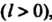, так как числитель и знаменатель в последней формуле одного знака. В этом случае говорят, что точка М делит отрезокВнутренним образом. Если

Точка М лежит вне отрезка, то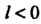(числитель и знаменатель в формуле

Имеют противоположные знаки); точка М делит отрезок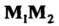Внешним образом.

Если точки Л/, и М совпадают, то

Пусть— точки координатной оси Ох, тогда

(1.4)

Откуда

(1.5)

Эта формула определяет координату точки М, делящей направленный отрезок 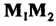В данном отношении I.

Если точка М совпадает с серединой отрезка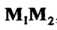, то, поэтому ее ко

Ордината определяется формулой

(16)

Пример 1.1. Даны две точки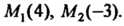Найти величину направленно

Го отрезка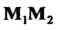И расстояние между точками.

В данном случаеПо формулам (1.1) и (1.2) находим

< Предыдущая		Следующая >