09. Знакочередующиеся ряды

Знакочередующийся ряд можно записать в виде:

Где

Признак Лейбница.

Если у знакочередующегося ряда абсолютные величины ui убывают и общий член стремится к нулю , то ряд сходится.

Признаки Даламбера и Коши для знакопеременных рядов.

Пусть - знакопеременный ряд.

Признак Даламбера. Если существует предел 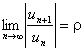, то при r<1 ряд будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.

Признак Коши. Если существует предел , то при r<1 ряд будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.

Пример. Разложить в ряд функцию

При помощи интегрирования.

При получаем по приведенной выше формуле:

Разложение в ряд функции может быть легко найдено способом алгебраического деления аналогично рассмотренному выше примеру.

Тогда получаем: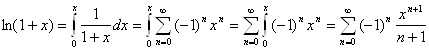

Окончательно получим:

< Предыдущая		Следующая >