2.7. Преобразование Фурье распределений
Выше (2.2.) установлено, что преобразование Фурье есть обратимое
Линейное преобразование (автоморфизм) пространства 
функций быстро убывающих вместе со всеми производными, 
. Поэтому оно является и автоморфизмом сопряженного пространства 
Умеренных распределений 
. Представляет интерес явное вычисление преобразований Фурье некоторых умеренных распределений. Прежде всего, если 
– распределение с ограниченным носителем, 
, то
и 
является Функцией 
, задаваемой формулой 
. Для распределений с носителем в точке это дает
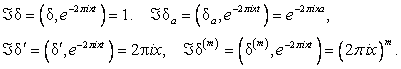(9)
Ясно, что
, найдем 
. Имеем 
. Отсюда следует 
. Найдем 
, вычислив двумя способами 
:
,
Откуда 
и 
. Аналогично можно обратить остальные формулы (9)
(10)
Наконец, пусть 
- сумма дельта – функций, расположенных в целых точках оси 
. Тогда
,
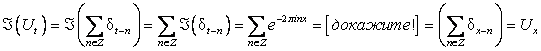То есть распределение , так же как и функция Гаусса 
(5), совпадает со своим преобразованием Фурье (формула суммирования Пуассона).
| < Предыдущая |
|---|
