26. Решение системы линейных уравнений
А) Последовательность действий для решения системы линейных уравнений методом Крамера такова:
Q создать матрицу коэффициентов системы линейных уравнений, например, 
(см. краткие теоретические сведения темы 2);
Q создать вектор свободных членов, например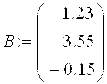 
;
Q с помощью оператора «:=» создать матрицу, равную матрице коэффициентов, например, 
;
Q заменить в созданной матрице первый столбец вектором свободных членов, используя операцию выделения столбца матрицы, например, 
или 
(в зависимости от значения переменной ORIGIN);
Q аналогично из матрицы коэффициентов создать матрицу, в которой второй столбец заменен вектором свободных членов, затем матрицу, в которой третий столбец заменен вектором свободных членов, и т. д. (количество таких матриц определяется количеством неизвестных в системе уравнений);
Q найти первый корень, разделив определитель матрицы с замененным первым столбцом на определитель матрицы коэффициентов, например: 
;
Q найти остальные корни системы уравнений аналогично.
Б) Последовательность действий для решения системы линейных уравнений матричным методом такова:
Q создать матрицу коэффициентов системы линейных уравнений, например, А (см. краткие теоретические сведения темы 2);
Q создать вектор свободных членов системы линейных уравнений, например, B;
Q получить решение системы с помощью функции Lsolve, параметрами которой являются матрица коэффициентов и вектор свободных членов, например: 
(решение также можно получить, умножив матрицу, обратную к матрице коэффициентов, на вектор свободных членов: 
);
Q вывести полученный вектор, содержащий корни системы, с помощью оператора «=».
В) Последовательность действий для решения системы линейных уравнений блочным методом такова:
Q задать начальные приближения для всех неизвестных, входящих в систему уравнений;
Q набрать ключевое слово Given;
Q ниже слова Given набрать уравнения, отделяя правую и левую части символом логического равенства «=» (см. краткие теоретические сведения темы 6);
Q набрать функцию Find, подставляя в качестве аргументов имена неизвестных системы;
Q вывести вектор, содержащий вычисленные значения корней, с помощью оператора «=», например Find(X1,X2,X3)=.
Замечание. Корни системы уравнений, полученные разными способами, должны совпасть.
Пример 6.3. Решить систему линейных уравнений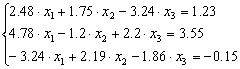 
методом Крамера, матричным и блочным методами. Сравнить полученные результаты. Начальные значения корней при использовании блочного метода принять равными 1.
Реализация в MathCad:
|
|
|
| < Предыдущая | Следующая > |
|---|
