25. Поиск корней полиномиального уравнения, графическая интерпретация
Последовательность действий для нахождения корней полиномиального уравнения вида ![]() с использованием функции Polyroots такова:
с использованием функции Polyroots такова:
Q создать вектор длиной (N+1), состоящий из коэффициентов полинома, расположенного в левой части уравнения (первый элемент - значение коэффициента полинома при х0, второй элемент - значение коэффициента полинома при х1 и т. д. и присвоить его какой-либо переменной (см. тему 2 и краткие теоретические сведения темы 6);
Q используя имя вектора в качестве аргумента функции Polyroots, получить числовые значения корней полиномиального уравнения с помощью оператора «=».
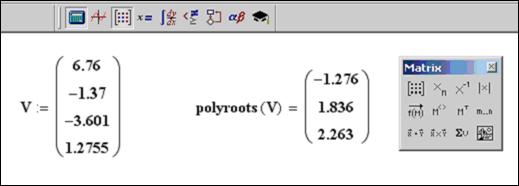
Пример 6.2. Вычислить множество корней полиномиального уравнения ![]() с использованием функции Polyroots.
с использованием функции Polyroots.
Реализация в MathCad:
| < Предыдущая | Следующая > |
|---|