2.4. Функции Ляпунова и теорема Ляпунова об устойчивости

Будем рассматривать систему (4.1) из предыдущего параграфа в окрестности точки покоя . Сформулируем теорему Ляпунова об устойчивости.

Если существует непрерывно дифференцируемая функция такая, что

1) в окрестности начала координат, за исключение точки , где ;

2) 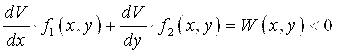, то точка покоя системы (4.1) устойчива.

Если обращается в нуль лишь при , то точка покоя асимптотически устойчива.

Функция при этом называется функцией Ляпунова, а называется производной от функции Ляпунова по времени, вычисленной в силу системы (4.1) и обозначается :

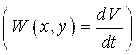Теорема Ляпунова дает метод установления устойчивости точки покоя системы путем подбора соответствующей функции .

Решение примеров.

Установить устойчивость точки покоя .

Рассмотрим функцию ,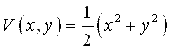

в окрестности начала за исключением самого начала. Поэтому все условия теоремы Ляпунова выполнены. Точка покоя системы асимптотически устойчива. Заметим, что установить устойчивость по первому приближению в данном случае невозможно, так как один из корней характеристического уравнения равен нулю.

Рассмотрим ,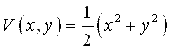

Как и в предыдущем случае устанавливаем, что в силу теоремы Ляпунова точка покоя устойчива асимптотически:

всюду, за исключением начала координат.

Уравнения первого приближения

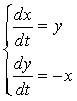
Имеют характеристическое уравнение вида

Все корни чисто мнимые, поэтому теоремы об устойчивости по первому приближению не дают ответа на вопрос об устойчивости.

< Предыдущая