11. Дифференциалы первого и высших порядков

Дифференциалом первого порядка функции Называется главная, линейная относительно аргумента часть. Дифференциалом аргумента называется приращение аргумента:.

Дифференциал функции равен произведению ее производной на дифференциал аргумента:

.

Основные свойства дифференциала:

Где .

Если приращение Аргумента мало по абсолютной величине, то и .

Таким образом, дифференциал функции может применяться для приближенных вычислений.

Дифференциалом второго порядка функции называется дифференциал от дифференциала первого порядка: .

Аналогично: .

.

Если и - независимая переменная, то дифференциалы высших порядков вычисляются по формулам

.

Пример.

Найти дифференциалы первого и второго порядков функции

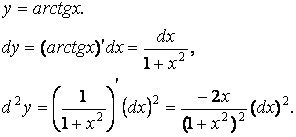
< Предыдущая		Следующая >