6.3.1. Примеры
Ниже приведены примеры неопределённостей, для раскрытия которых удобно пользоваться таблицами эквивалентных бесконечно малых, полученных в качестве следствий 1 и 2 замечательных пределов, или непосредственно самими этими пределами.
При использовании эквивалентных бесконечно малых следует помнить, что Разность двух бесконечно малых – бесконечно малая более высокого порядка малости, чем каждая из них: ![]() , то
, то ![]() . Заменять эквивалентными в такой разности непосредственно нельзя. Такое выражение должно быть предварительно преобразовано.
. Заменять эквивалентными в такой разности непосредственно нельзя. Такое выражение должно быть предварительно преобразовано.
Пример 1.
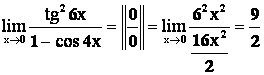 .
.
Пример 2.
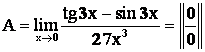
Решение. Обратите внимание, что ![]() . Замена
. Замена ![]() и
и ![]() на
на ![]() привела бы к неправильному результату. Разность
привела бы к неправильному результату. Разность ![]() должна быть предварительно преобразована:
должна быть предварительно преобразована:
![]()
Тогда ![]() .
.
Пример 3.
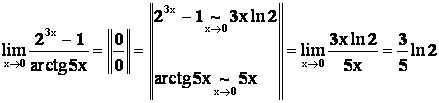 .
.
Пример 4.
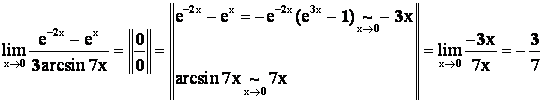 .
.
Пример 5.
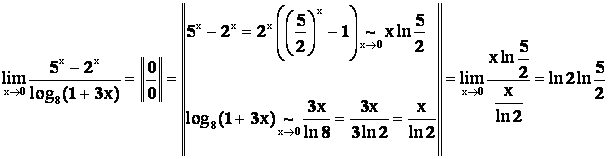
Пример 6.

Пример 7.
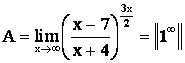
Решение. При раскрытии неопределенностей вида ![]() следует воспользоваться вторым замечательным пределом
следует воспользоваться вторым замечательным пределом 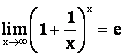 .
.
Анализ выражения, стоящего под знаком 2 замечательного предела, показывает, что его конструкция такова: к единице прибавляется бесконечно малая величина ![]() и эта сумма возводиться в степень, равную обратной величине для прибавляемой бесконечно малой, т. е. х или
и эта сумма возводиться в степень, равную обратной величине для прибавляемой бесконечно малой, т. е. х или ![]() . Если в данном примере к основанию степени мы прибавим и отнимем единицу, то выражение не изменится, но мы сможем определить вид прибавляемой бесконечно малой величины. Т. е.
. Если в данном примере к основанию степени мы прибавим и отнимем единицу, то выражение не изменится, но мы сможем определить вид прибавляемой бесконечно малой величины. Т. е.
![]() .
.
Таким образом, роль бесконечно малой ![]() играет слагаемое
играет слагаемое ![]() , которое стремится к 0 при
, которое стремится к 0 при ![]() . Обратная величина
. Обратная величина ![]() будет
будет ![]() . Выполним тождественное преобразование.
. Выполним тождественное преобразование.
 .
.
Предел основания в полученном выражении равен числу Е, т. е.
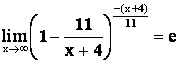 (по 2 замечательному пределу).
(по 2 замечательному пределу).
Тогда данный предел сводиться к вычислению предела показателя, т. е.
 .
.
В результате проведенного анализа можно сделать вывод, что если ![]() – бесконечно малая, а
– бесконечно малая, а ![]() Бесконечно большая в расматривамом процессе (
Бесконечно большая в расматривамом процессе (![]() Или
Или ![]() ), то
), то ![]()
Пример 8.
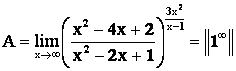
Решение. Выполним преобразование с основанием и показателем степени (См. пример 7.)
Тогда
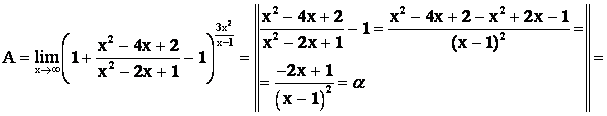

Замечание. Если воспользоваться выводом из примера 7, то можно сразу записать, что
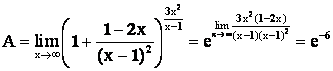 .
.
Пример 9.
![]()
Решение.
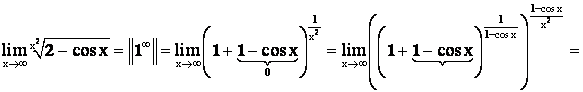
![]() .
.
Следует заметить, что если бесконечно малые ![]() и
и ![]() эквивалентны и бесконечно большие
эквивалентны и бесконечно большие ![]() и
и ![]() Эквивалентны, то
Эквивалентны, то ![]()
Этот факт существенно упрощает вычисление пределов при раскрытии неопределенностей вида ![]()
Так, если учесть, что ![]() , то последний пример можно было решать следующим образом
, то последний пример можно было решать следующим образом
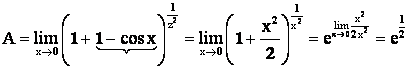 .
.
Пример 10.
![]() .
.
Решение. 1 способ:
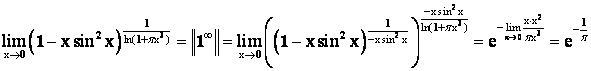
2 способ:
Так как ![]() , а
, а 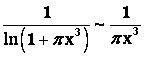 , то
, то
![]() .
.
Ниже рассмотрены пределы при условии, что ![]() , тогда
, тогда ![]() . В этих случаях удобна замена переменной
. В этих случаях удобна замена переменной ![]() , т. е. получение возможности непосредственного использования таблицы эквивалентных бесконечно малых величин для выделения «главных частей».
, т. е. получение возможности непосредственного использования таблицы эквивалентных бесконечно малых величин для выделения «главных частей».
Пример 1.
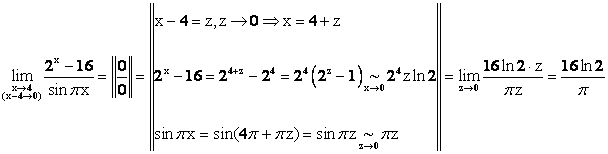 Пример 2.
Пример 2. 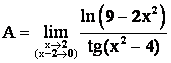
Решение. 1 способ.
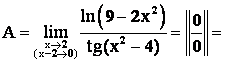
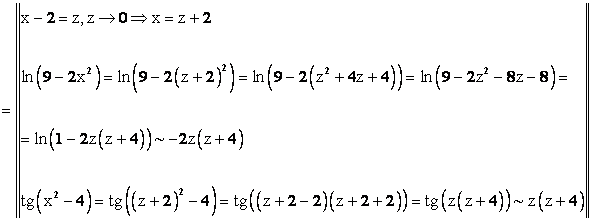
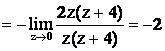 .
.
2 способ. Следует заметить, что замену переменной можно было бы не делать. Так как при ![]() величина
величина ![]() , т. е. является бесконечно малой, то
, т. е. является бесконечно малой, то ![]() .
.
Преобразуем числитель
![]() при
при ![]() .
.
Тогда 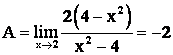 .
.
Пример 3.
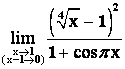
Решение.
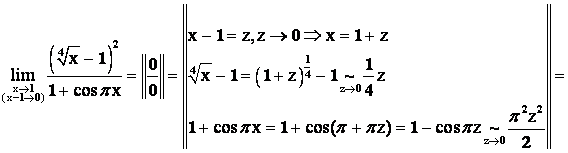
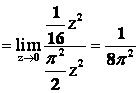 .
.
Пример 4.
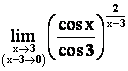
Решение.

![]() .
.
Пример 5.
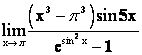
Решение.
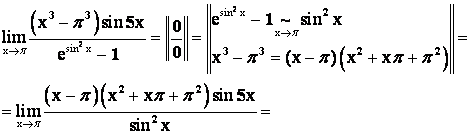
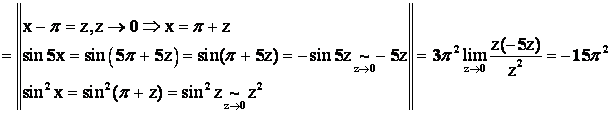
Пример 6.
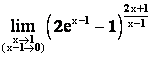
Решение.
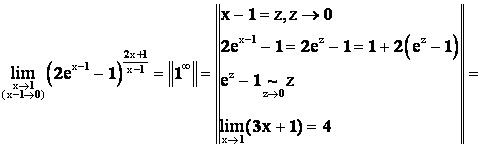
![]()
Пример 7.
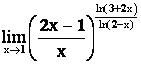
Решение.

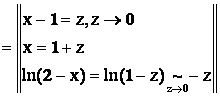 =
= .
.
Пример 8.
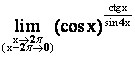
Решение.
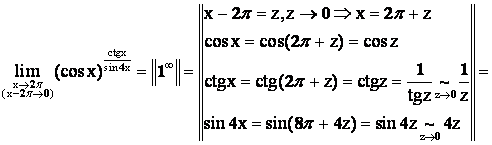
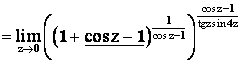
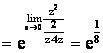 .
.
| < Предыдущая | Следующая > |
|---|