15. Примеры решения задач 4
Пример 4.1. По имеющимся данным о сбыте продукции (в тыс. руб.) в различных фирмах города рассчитать абсолютные и относительные показатели вариации.
87, 75, 66, 60, 87, 67, 66, 69, 89, 74, 90, 78, 99, 86, 76, 95, 69, 68, 87, 63.
Решение (см. пример 3.7).
Рассчитаем абсолютные показатели вариации.
Размах R=Xmax – Xmin=99–60=39.
Квартильный размах IQR=Q3 –Q1=87–67,5=19,5.
Средняя арифметическая ![]() .
.
Поскольку представленные данные не сгруппированы, применим невзвешенные формулы показателей вариации:
Среднее линейное отклонение
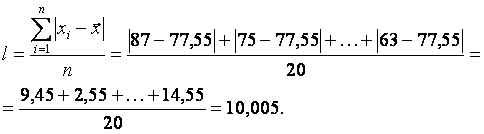 ,
,
Дисперсия
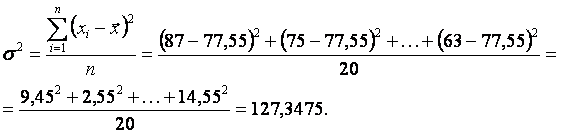
Среднее квадратическое отклонение
![]()
Относительные показатели вариации.
Относительный размах 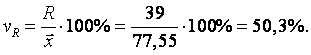
Относительное квартильное расстояние

Относительное линейное отклонение
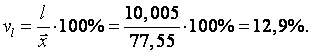
Коэффициент вариации

Можно сделать вывод, что вариация признака в совокупности небольшая, совокупность можно считать однородной по данному признаку.
Пример 4.2. Произвести группировку данных примера 4.1, образовав 4 равных интервалов. По полученному интервальному ряду определить абсолютные и относительные показатели вариации.
Решение (см. пример 3.8).
В таблице приведены результаты группировки исходных данных.
|
Номер группы |
Границы группы |
Частота, Fi |
Середина интервала, Xi |
|
|
|
|
|
1 |
До 70 |
8 |
65 |
12,5 |
100 |
156,25 |
1250 |
|
2 |
70–80 |
4 |
75 |
2,5 |
10 |
6,25 |
25 |
|
3 |
80–90 |
3 |
85 |
7,5 |
22,5 |
56,25 |
168,75 |
|
4 |
Более 90 |
5 |
95 |
17,5 |
87,5 |
306,25 |
1531,25 |
|
Итого |
20 |
220 |
2975 |
Для расчета обобщающих показателей по результатам группировки применим взвешенные формулы средней арифметической и показателей вариации.
Средняя арифметическая, найденная по сгруппированным данным
![]() .
.
Рассчитаем абсолютные показатели вариации.
Размах R=Xmax – Xmin=100–60=40.
Квартильный размах IQR=Q3 –Q1=90–66,25=23,75.
Среднее линейное отклонение 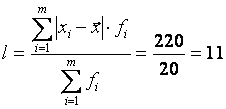 .
.
Дисперсия
 .
.
Среднее квадратическое отклонение
![]()
Относительные показатели вариации.
Относительный размах VR= 40/77,5×100%=51,61%.
Относительное квартильное расстояние Vq= 23,75/77,5×100%= =30,65%.
Относительное линейное отклонение Vl= 11/77,5×100%=14,19%.
Коэффициент вариации V= 12,196/77,5×100%=15,74%.
E Обратите внимание, что полученные значения показателей вариации отличаются в зависимости от того, какие данные (сгруппированные или несгруппированные) были использованы. Более точные результаты получаются для несгруппированных данных.
Как и в примере 4.1, можно сделать вывод об однородности совокупности по данному признаку.
Пример 4.3. На основании данных о доходах населения определить, влияет ли место жительство человека уровень его доходов.
|
Доход, тыс. руб./чел. |
Жители города А |
Жители города Б |
|
До 5 |
2 |
1 |
|
5–10 |
19 |
3 |
|
10–15 |
15 |
6 |
|
15–20 |
10 |
10 |
|
20–25 |
3 |
13 |
|
25 и выше |
1 |
7 |
Решение. В таблицах приведены промежуточные расчеты.
|
Доход, тыс. руб./чел. |
Жители |
Середина |
Xi×Fi |
|
|
|
До 5 |
2 |
2,5 |
5 |
90,25 |
180,5 |
|
5–10 |
19 |
7,5 |
142,5 |
20,25 |
384,75 |
|
10–15 |
15 |
10,5 |
187,5 |
0,25 |
3,75 |
|
15–20 |
11 |
17,5 |
192,5 |
30,25 |
332,75 |
|
20–25 |
2 |
22,5 |
45 |
110,25 |
220,5 |
|
25 и выше |
1 |
27,5 |
27,5 |
240,25 |
240,25 |
|
Итого |
50 |
600 |
1362,5 |
|
Доход, тыс. руб./чел. |
Жители |
Середина |
Xi×Fi |
|
|
|
До 5 |
1 |
2,5 |
2.5 |
272.25 |
272.25 |
|
5–10 |
3 |
7,5 |
22.5 |
132.25 |
396.75 |
|
10–15 |
6 |
10,5 |
75 |
42.25 |
253.5 |
|
15–20 |
10 |
17,5 |
175 |
2.25 |
22.5 |
|
20–25 |
13 |
22,5 |
292.5 |
12.25 |
159.25 |
|
25 и выше |
7 |
27,5 |
192.5 |
72.25 |
505.75 |
|
Итого |
40 |
760 |
1610 |
1. Групповые средние (среднедушевой доход):
![]() =600/50=12 тыс. руб./ чел.
=600/50=12 тыс. руб./ чел.
![]() =760/40=19 тыс. руб./ чел.
=760/40=19 тыс. руб./ чел.
2. Внутригрупповые дисперсии:
![]() =1362,5/50=27,25.
=1362,5/50=27,25.
![]() =1610/40=40,25.
=1610/40=40,25.
3. Средняя из внутригрупповых дисперсий:
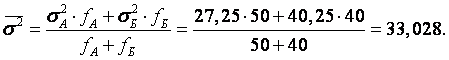
4. Для расчета межгрупповой дисперсии сначала определим общую среднюю как среднюю арифметическую взвешенную из групповых средних:
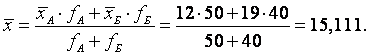
Тогда межгрупповая дисперсия
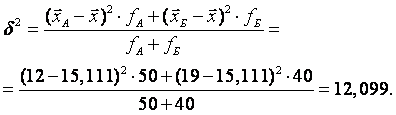
5. Общую дисперсию найдем по правилу сложения дисперсий
![]()
Коэффициент детерминации и эмпирическое корреляционное отношение равны соответственно


Согласно шкале Чэддока можно сделать вывод, что местожительство «заметно» влияет на доходы населения.
| < Предыдущая | Следующая > |
|---|