14. Правило сложения дисперсий

Вариация значений признака обусловлена как воздействием случайных факторов (случайная вариация), так и воздействием неслучайных факторов (систематическая вариация). Изучение вариации позволяет вскрыть сущность изучаемого явления – выявить каковы существенные факторы и оценить степень их влияния.

Для оценки влияние отдельных факторов на вариацию осуществляют группировку, разбивая изучаемую совокупность на группы, однородные по изучаемому признаку. Изучение вариации проводят путем исчисления и анализа следующих видов дисперсий: общей, межгрупповой и внутригрупповой.

Общая дисперсия измеряет вариацию признака, обусловленную влиянием всех факторов (случайных и неслучайных) на данную совокупность. Может быть рассчитана по формуле простой (4.6) или взвешенной (4.7) дисперсии.

Межгрупповая дисперсия измеряет систематическую вариацию, т. е. оценивает влияние признака-фактора, положенного в основание группировки, на вариацию изучаемого (результативного) признака.

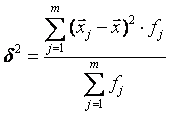(4.14)

Где – групповая (частная) средняя J-й группы; – общая средняя всей совокупности; Fj – частота J-й группы.

Внутригрупповые (частные) дисперсии отражают случайную вариацию, т. е. часть вариации, обусловленную влиянием других неучтенных факторов. Внутригрупповая дисперсия J-й группы вычисляется на основе отклонений отдельных значений признака внутри J-й группы от средней арифметической этой группы. В зависимости от имеющихся данных может использоваться формула простой (4.6) или взвешенной дисперсии (4.7).

Средняя из внутригрупповых дисперсий – Это средняя арифметическая взвешенная из внутригрупповых дисперсий.

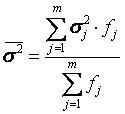. (4.15)

Согласно Правилу сложения дисперсий общая дисперсия равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий

. (4.16)

Правило сложения дисперсий позволяет оценить степень влияния группировочного признака-фактора на изучаемый результативный показатель. Для оценки тесноты связи этих факторов служат Коэффициент детерминации и Эмпирическое (выборочное) корреляционное отношение.

Коэффициент детерминации

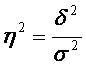. (4.17)

Эмпирическое (выборочное) корреляционное отношение

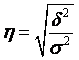. (4.18)

Коэффициент детерминации H2 и эмпирическое корреляционное отношение H принимают значения в диапазоне от 0 до 1. При отсутствии влияния группировочного признака-фактора на вариацию результативного показателя эти показатели равны нулю. Чем ближе значения показателя к единице, тем сильнее связь.

Для качественной оценки тесноты связи на основе показателя эмпирического корреляционного отношения H использовать шкалу Чэддока:

H	0,1–0,3	0,3–0,5	0,5–0,7	0,7–0,9	0,9–0,99
Теснота связи	Слабая	Умеренная	Заметная	Тесная	Весьма тесная

< Предыдущая		Следующая >