03.1. Случайная величина и ее распределение

Случайной величиной наЗЫвается переменная, которая может принимать в зависимости от исходов испытания те или иные случайные значения.

Если при этом переменная принимает последовательные различные значения и известны вероятности каждого из них; то она называется Дискретной случайной величиной. Дискретная случайная величина Х определена, если даны все ее возможные значения , число которых может быть как конечным, так и бесконечным, и соответствующие вероятности

Это задание представляется таблицей Распределения,

			…
			…

В котороЙ значения Х располагаются в строго возрастающем порядке. При этом сумма соответствующих этИМ значениям вероятностей равна 1, так как все возможные значения случайной величины представляют полную систему событий.

В случае конечного числа K возможных значений эта сумма запишется в виде

Для дискретной случайной величины с бесконечным множеством возможных значений эта сумма будет представлять собой ряд.

Представленная в виде таблицы совокупность всех значений случайной величины и соответственных вероятностей каждой из них или, что то же, функция Р(х), связывающая значения с соответствующими вероятностями, является Законом распределения случайной величины.

Примерами дискретных случайных величин являются:

1) число грузовых машин, проезжающих за один час через контрольный пункт автоинспекции;

2) сумма выигрыша, приходящегося на один билет денежно-вещевой лотереи;

3) число ничейных результатов в шахматном турнире;

4) число отличных оценок у студентов одной группы на экзамене.

Пример 1. Составить закон распределения случайной величины — числа появлений события А при П повторных независимых испытаниях, если вероятность появления этого события в отдельном испытании очень мала.

Решение. Вероятность появления события А M раз в испытаниях определяется формулой Пуассона

Соответствующая таблица распределения имеет такой вид:

Т	0	1	2	…	Т	…
				…		...

Можно показать, что при неограниченном возрастании числа П сумма вероятностей в этом распределении представляет ряд, сходящийся к 1:

Пример 2. По мишени ведутся выстрелы до первого попадания или до Израсходования всех имеющихся патронов. Составить таблицу распределения случайной величины Х — Числа израсходованных патронов, если вероятность попадания при отдельНОм выстреле постоянна, Р=0,3, а число всех патронов .

Решение. Здесь случайная величина Х принимает значения: при попадании с одного выстрела, — При попадании после одного промаха, — При попадании после двух промахов и — при четырех промахах или при попадании после трех промахов. Вероятности того, что случайная величина Х будет принимать указание значения, таковы:

и

Отсюда получаем искомую таблицу распределения

	1	2	3	4
	0.3	0.21	0.147	0.343

Условие выполнено.

График, соответствующий заданному распределению, называется Многоугольником распределения случайной величины. При этом по оси абсцисс откладываются значения х; случайной величины, а по оси ординат - их вероятности .

В качестве примера распределения случайной величины можно взять еще рассмотренное нами биномиальное распределение вероятностей числа пригодных деталей среди взятых наудачу 6 деталей

Здесь случайной величиной является число пригодных деталей со следующим законом распределения:

	0	1	2	3	4	5	6
	0.0002	0.0041	0.033	0.132	0.297	0.3558	0.1779

Многоугольник распределения этой случайной величины графически совпадает с многоугольником, изображенным на рис. 2, с оговоркой, что по оси абсцисс откладываются значения случайной величины (количества пригодных деталей).

Помимо дискретных существуют еще Непрерывные случайные величины, которые могут принимать все значения в заданных границах (внутри некоторого отрезка) или на всей числовой оси. Приведем примеры непрерывных случайных величин:

1) расстояние точки падения диска от точки метания;

2) периметр перпендикулярного сечения ствола дерева;

3) расстояние от центра мишени до точки попадания пули при стрельбе.

Для непрерывной случайной величины нельзя составить таблицы, в которой были бы перечислены все ее значения даже в небольшом интервале. Поэтому закон ее распределения должен определять вероятность попадания ее значений в некоторый отрезок.

Пусть дана непрерывная случайная величина X. Тогда условие Х < Х для ее значений можно рассматривать как событие, вероятность наступления которого является некоторой функцией Х. Обозначив эту функцию через F(Х), будем иметь

F(X)=P(X<X).

F(Х) называют Функцией распределения вероятностей случайной величины, или интегральной функцией распределения1). Будем предполагать эту функциЮ непрерывной.

Отметим свойства функции F(X).

1°. Исходя из возможных значений вероятности, имеем

2°. При имеем , так как

Отсюда F(X) — Функция неубывающая.

3°. Условие для значений случайной величины является достоверным событием, следовательно, .

4°. Условие невозможно; поэтому .

Выразим с помощью введенной функции вероятность того, что случайная величина Х удовлетворяет условию , т. е. найдем .

Так как , то условие означает, что или , или .

Отсюда на основании теоремы сложения вероятностей имеет место равенство

Здесь второе слагаемое

.

Но для непрерывной случайной величины вероятность того, что она примет какое-либо определенное значение, равна нулю и, в частности, .

Справедливость этого следует из непрерывности F(X). Действительно, если в равенстве

Принять и перейти к пределу, то найдем, что

Поэтому

И соответственно

.

Отсюда

.

Таким образом,

.

Этим определена вероятность того, что случайная величина принимает какое-то (безразлично какое) значение внутри отрезка в виде приращения функции F(Х) на всем этом отрезке.

Для дискретной случайной величины также можно определить функцию распределения. Ее значения легко находятся по таблице в виде суммы вероятностей тех значений случайной величины, которые удовлетворяют условию для каждого значения Х.

Пример 3. Составить функцию распределения для дискретной случайной величины Х — Числа появлений события А при 4 независимых испытаниях, если в каждом испытании .

Решение. Определив по формуле Бернулли значения вероятностей при I=0, 1, 2, 3 и 4, составим таблицу распределения

	0	1	2	3	4

По данным этой таблицы определяем

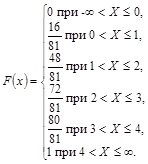
Функция F(X) для дискретной случайной величины является кусочно-постоянной с точками разрыва при всех . График функции распределения для рассмотренного примера (рис. 5) наглядно отражает характер (ступенчатый) функции распределения дискретной случайной величины.

Рис. 5

Помимо рассмотренной функции распределения, представляющей интегральный закон, для характеристики непрерывной случайной величины применяется еще Дифференциальный закон распределения, Связанный с понятием ПлоТНости распределения вероятностей случайной величины.

Если с изменением длины отрезка вероятность попадания случайной величины Х в этот отрезок меняется пропорционально длине отрезка, т. Е. , то говорят, что случайная величина Х равномерно распределена в промежутке . При этом отношение

— величина постоянная.

Это отношение по аналогии со случаем равномерного распределения массы (в механике) называют Плотностью распределения вероятностей равномерно распределенной случайной величины.

Если при этом границы отрезка включают все возможные значения случайной величины X, то условие — событие достоверное. Тогда ,

И соответственно плотность вероятности

Если случайная величина не является равномерно распределенной, то приведенное отношение выражает среднюю плотность распределения вероятностей в данном промежутке, и тогда вводится понятие Плотности распределения вероятностей в точке.

Эта «плотность», как и в механике, определяется производной от функциИ F(Х) в точке Х:

Функция , выражающая плотность распределения вероятностей, называется Дифференциальной функцией распределения вероятностей и представляет дифференциальный закон распределения.

Переходя к дифференциалу как к главной части приращения функции, будем иметь

Это значит, что произведение приближенно определяет вероятность того, что случайная величина Х принимает некоторое значение в промежутке .

Таким образом, установлено, что если функция Р(Х), выражающая интегральный закон распределения вероятностей, дает точное значение вероятности попадания случайной величины в промежуток, то плотность вероятности , выражающая дифференциальный закон распределения, дает здесь приближенное значение.

В теоретических исследованиях и при решении практических задач часто бывает удобней пользоваться дифференциальным законом распределения.

В порядке иллюстрации изложенных сведений о распределении непрерывной случайной величины можно, например, отметить, что при равномерном распределении случайной величины на отрезке Плотность ее вероятности (рис. 6, а) изображается прямой, параллельной оси Ох, а функция распределения F(X) (рис. 6, б) — отрезком прямой, проходящей через точки и . ЗдесЬ

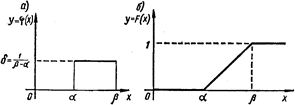
Рис. 6 а Рис. 6 б

Если непрерывная случайная величина задана плотностью , то график функции называется Кривой распределения вероятностей этой случайной величины (рис. 7). При этом вероятность определяется площаДью криволинейной трапеции, заключенной между кривой, осью абсцисс и прямыми и .

Если непрерывная случайная величина задана функцией распределения F(Х), то ее график называется Интегральной кривой расПределения (рис. 8). При этом вероятность Определяется приращением ординаты этой кривой .

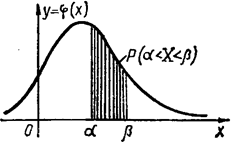
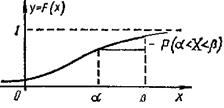
Рис. 7 Рис. 8

В рамках настоящего курса не рассматриваются различные виды распределения вероятностей, кроме нормального распределения, основные сведения о котором будут даны ниже.

< Предыдущая		Следующая >