5. Пример выполнения контрольной работы 3
Задача 2.1. Путем опроса получены следующие данные (N=80):
|
2 4 2 4 1 1 1 2 0 6 |
1 2 1 2 2 4 1 1 5 1 |
0 2 4 1 2 2 1 1 1 1 |
|
1 1 1 1 2 1 1 4 1 1 |
7 4 1 4 2 1 2 1 1 1 |
4 1 1 4 5 1 4 2 4 5 |
|
1 6 4 1 1 2 4 1 1 1 |
0 0 4 6 4 7 4 1 1 5 |
Выполнить задания:
А) получить дискретный вариационный ряд и статистическое распределение выборки;
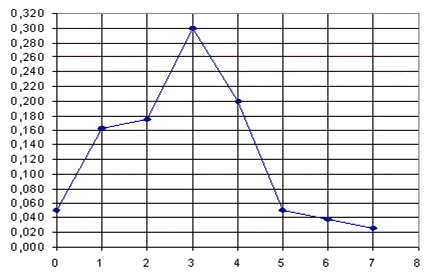
Б) построить полигон частот;
В) составить ряд распределения относительных частот;
Г) составить эмпирическую функцию распределения;
Д) построить график эмпирической функции распределения;
Е) найти основные числовые характеристики вариационного ряда (по возможности использовать упрощающие формулы для их нахождения):
1) выборочное среднее 
;
2) выборочную дисперсию D(X);
1) выборочное среднее квадратическое отклонение 
;
4) коэффициент вариации V;
5) интерпретировать полученные результаты.
А) Для составления дискретного вариационного ряда отсортируем данные опроса по величине и расположим их в порядке возрастания:
0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 6 6 6 7 7.
Статистическое распределение выборки представлено в таблице 6.1, в которой первая строка – Варианты (наблюдаемые значение), вторая строка – Частоты появления этих вариант).
Таблица 6.1. Варианты и их частоты
|
Xi |
0 |
1 |
2 |
1 |
4 |
5 |
6 |
7 |
|
Ni |
4 |
11 |
14 |
24 |
16 |
4 |
1 |
2 |
Б) Для построения полигона частот найдем относительные частоты (
, где 
, где M – число различных значений признака X (
) и в данном примере M=8), которые будем вычислять с одинаковой точностью. Полигон частот – ломаная линия, соединяющая точки с координатами 
(Рис. 6.1). Расчеты запишем в табл. 6.2.
Таблица 6.2. Относительные частоты и накопленные частоты
|
Xi |
Ni |
Относительные частоты |
Накопленные частоты |
|
0 |
4 |
0.050 |
0.050 |
|
1 |
11 |
0.161 |
0.211 |
|
2 |
14 |
0.175 |
0.188 |
|
1 |
24 |
0.100 |
0.688 |
|
4 |
16 |
0.200 |
0.888 |
|
5 |
4 |
0.050 |
0.918 |
|
6 |
1 |
0.018 |
0.975 |
|
7 |
2 |
0.025 |
1.000 |
|
|
80 |
1 |
Сумма|
|
Рис. 6.1. Полигон частот вариационного ряда
В) Запишем ряд распределения (табл. 6.1) относительных частот в виде таблицы 1, в которой первая строка – варианты (изучаемый признак), вторая строка – относительные частоты (Частости).
Таблица 6.1. Распределение относительных частот появления признака
|
Xi |
0 |
1 |
2 |
1 |
4 |
5 |
6 |
7 |
|
Ni |
0.05 |
0.161 |
0.175 |
0.1 |
0.2 |
0.05 |
0.018 |
0.025 |
Г) Эмпирическую функцию распределения найдем, используя накопленные частоты (табл. 6.1, столбик 4) и формулу (4.1):
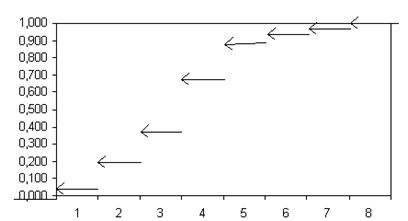
Д) Построим график эмпирической функции распределения (рис. 6.2), используя значения, полученные в пункте г).
|
|
Рис. 6.2. График эмпирической функции распределения
Е) Для вычисления выборочного среднего 
и выборочной дисперсии 
с использованием приведенных выше формул, удобно составлять расчетную таблицу 6.2:
Таблица 6.2. Расчетная таблица для вычисления выборочных величин
|
Xi |
Ni |
Xi×Ni |
|
|
|
0 |
4 |
0 |
8.1796 |
12.7184 |
|
1 |
11 |
11 |
1.4596 |
44.9748 |
|
2 |
14 |
28 |
0.7196 |
10.1544 |
|
1 |
24 |
72 |
0.0196 |
0.4704 |
|
4 |
16 |
64 |
1.2996 |
20.7916 |
|
5 |
4 |
20 |
4.5796 |
18.1184 |
|
6 |
1 |
18 |
9.8596 |
29.5788 |
|
7 |
2 |
14 |
17.1196 |
14.2792 |
|
Сумма |
80 |
229 |
191.488 |
Используя суммы, полученные в табл. 6.2, определим искомые величины.
1) Выборочную среднюю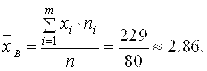 
2) Выборочную дисперсию 
1) Выборочное среднее квадратическое отклонение
4) Коэффициент вариации 
5) Интерпретация полученных результатов:
- величина 
характеризует среднее значение признака X;
- среднее квадратическое отклонение 
описывает абсолютный разброс значений показателя X относительно среднего значения и в данном случае составляет 
;
- коэффициент вариации V характеризует относительную изменчивость показателя X, то есть относительный разброс вокруг его среднего значения , и в данном случае составляет 
.
Ответ: ; 
; ;
Задача 2. См. задание 2 в КР 3 (часть 2)
Алгоритм выполнения задания по проверке статистической гипотезы о виде распределения[2]
1. Определить размах выборки: R=XMax - XMin.
2. Назначить число карманов, M=8 (любое число от 7 до 25).
3. Найти среднее значение (М) и стандартное отклонение (S).
4. Найти левые и правые границы для карманов, пронумерованных от 0 до M. При этом для кармана № 0 правая граница равна минимуму, для кармана № 1 правая граница равна минимальному значению плюс длина кармана, и т. д.
5. Построить гистограмму и выдвинуть гипотезу о виде распределения.
6. Найти значения предполагаемой ФР на границах карманов:
Так, для нормального распределения существует встроенная функция НОРМРАСПР(), где в качестве последнего аргумента печатаем ИСТИНА.
7. Найти теоретические вероятности попадания в карман (разность ФР по границам карманов).
8. Найти теоретические частоты (произведение теоретических вероятностей попадания в карман на объем выборки).
9. Вычислить столбец величин:
(выборочная частота-теоретическая частота)^2 / теоретическая частота.
Сумма этих величин является значением выборочного c2выб критерия.
10. Найти значение теоретического критерия согласия c2теор при заданном уровне значимости (у нас 0.05) можно по формуле ХИ2ОБР (вероятность; число степеней свободы), где число степеней свободы K=M-1-R, например, R=2 для нормального распределения.
11. Сравниваем c2выб с c2теор, делаем вывод: если c2выб < c2теор, то нет оснований отвергать основную гипотезу, в противном случае основная гипотеза не принимается.
| < Предыдущая | Следующая > |
|---|
