2.05. Условная вероятность. Вероятность произведения событий
Определение 2.2. Вероятность события А, Вычисленная при условии, что произошло событие В, Называется Условной вероЯтностью события А при наличии события В И обозначается Р(А|В).
Пример 2.10. Опыт: подбрасывание двух монет. События:
А = {выпадение «орла» на обеих монетах};
В = {выпадение «орла» на одной из монет}.
Найти вероятность Р(А). Общее число возможных исходов опыта N=4 (Оо, Ор, рр, ро), благоприятствующий исход один (оо), следовательно, Р(А)=1/4.
Найти теперь условную вероятность Р(А|В). Поскольку известно, что произошло событие В, Число возможных исходов испытания П–1 (оо, ор, ро), благоприятствующий исход по–прежнему один, следовательно, Р(А|В)=1/3.
Теорема. Вероятность произведения двух событий А И В, Равна произведению вероятности одного из этих событий на условную вероятность другого при наличии первого:
Р(АВ) = Р(А)Р(В|А) или Р(АВ) = Р(В)Р(А|В). (2.1)
Эта теорема обобщается на любое конечное число событий следующим образом:
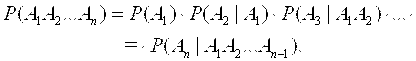 (2.2)
(2.2)
Определение 2.3. Два события называются независимыми, если появление любого из них не изменяет вероятности другого, т. е. события А И В Независимы, если Р(А|В)=Р(А).
Из формул (2.1) следует, что если выполняется равенство Р(А|В)=Р(А),.То выполняется и равенство Р(В\А)=Р(В).
Определение 2.4. Несколько событий, А1, А2, ..., Ап, Называются независимыми в совокупности (или просто независимыми), если появление любых из них не изменяет вероятностей остальных. Для независимых событий формула (2.2) принимает вид:
Р(А1 А2 ...Ап) = Р(А1)×Р(А2×...×Р(Ап).
Пример 2.11. Из урны, содержащей 3 белых и 7 черных шаров, наудачу извлекают два шара. Найти вероятность того, что оба шара белые.
Решение. Считаем, что шары извлекаются поочередно. Пусть
А = {первый шар – белый}, В = {второй шар – белый}, тогда АВ – {оба шара – белые}.
По теореме умножения вероятностей Р(АВ)=Р(А)Р(В|А). Согласно классическому определению вероятности Р(А)=3/10, Р(В|А)=2/9. Следовательно, Р(АВ)= (3/10)×(2/9).
Пример 2.12. Два стрелка стреляют по одной мишени. Вероятность поражения мишени первым стрелком равна 0.6, вторым – 0.8. Найти вероятность того, что в мишени будет две пробоины.
Решение. Введем в рассмотрение события, вероятности которых известны:
А = {поражение мишени первым стрелком},
В – {поражение мишени вторым стрелком}.
Интересующее нас событие выразим через эти события. Для того, чтобы имело место событие С={две пробоины в мишени}, надо, чтобы произошли вместе события А И В, Т. е. С=АВ.
Естественно считать события А И В Независимыми, поэтому
Р(С)=Р(А)×Р(В)=0.6×0.8.
| < Предыдущая | Следующая > |
|---|