2.03. Основные формулы комбинаторики

Комбинаторика – это раздел математики, посвященный решению задач выбора и расположения элементов конечного множества в соответствии с заданными правилами. В теории вероятностей формулы комбинаторики широко используются для подсчета числа исходов опыта.

Основной принцип комбинаторики. Пусть требуется выполнить одно за другим K Действий, причем первое действие можно выполнить П1, Способами, второе – П2 способами и т. д., тогда все K Действий можно выполнить следующим числом способов:

П = П1×П2×..×ПK.

Все приводимые ниже формулы комбинаторики выводятся как следствия из этого основного правила.

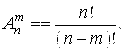
Сочетания. Пусть W – множество из П Элементов. Произвольное (Неупорядоченное) Т–Элементное подмножество множества из П Элементов называется Сочетанием из п элементов по т. Сочетаниями из трёх элементов по два являются следующие неупорядоченные подмножества множества {А, b, c}: {A, b},{A, c},{B, c}.

Число сочетаний из П Элементов по Т

Определение 2.1. Множество называется Упорядоченным, если каждому элементу этого множества поставлено в соответствие некоторое число (номер элемента) от 1 до П (п – число элементов множества) так, что различным элементам соответствуют различные числа.

Перестановки. Различные упорядоченные множества, которые отличаются лишь порядком элементов (т. е. могут быть получены из того же самого множества), называются Перестановками Этого множества. Например, перестановками множества {А, B, с} являются упорядоченные множества (А, B, С), (А, с, B), (B, а, с), (B, с, А), (С, а, B), (С, B, а).

Число перестановок из П Элементов

Рп =1×2×...× (N–1) N = N!

Размещения. Упорядоченное M–элементное подмножество множества из П Элементов называется размещением из П Элементов по Т. Например, размещениями из трёх элементов по два являются следующие упорядоченные подмножества множества (А, B, с): (А, B), (B, а), (А, с), (С, а), (B, с), (С, B).

Число размещений из П Элементов по Т

Пример 2.7. Набирая номер телефона, абонент забыл последние две цифры и, помня, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набран правильный номер.

Решение. Воспользуемся классическим определением вероятности. Общее число исходов испытания (выбор в определенном порядке двух цифр из десяти) равно числу вариантов извлечения двух элементов из десяти с учетом порядка следования их, т. е. числу размещений из десяти элементов по два:

Благоприятный исход испытания только один, Т=1. Следовательно, искомая вероятность равна P=1|90.

Пример 2.8. В партии из десяти деталей 7 стандартных. Найти вероятность того, что среди 6 взятых наудачу изделий 4 стандартных.

Решение. Общее число исходов испытания равно числу вариантов извлечения шести деталей из десяти без учета порядка извлечения, т. е. равно числу сочетаний из десяти элементов по шесть:

Число благоприятных исходов согласно основному правилу комбинаторики равно произведению числа вариантов извлечения четырех деталей из семи стандартных на число вариантов извлечения двух деталей из трех нестандартных:

Искомая вероятность равна Р= 105/210= 1/2.

< Предыдущая		Следующая >