3.04. Моделирование в условиях определенности

Классическим примером простейшей задачи системного анализа в условиях определенности может служить задача производства и поставок товара. Пусть некоторая фирма должна производить и поставлять продукцию клиентам равномерными партиями в количестве N =24000 единиц в год. Срыв поставок недопустим, так как штраф за это можно считать бесконечно большим.

Запускать в производство приходится сразу всю партию, таковы условия технологии. Стоимость хранения единицы продукции Cx=10 копеек в месяц, а стоимость запуска одной партии в производство (независимо от ее объема) составляет Cp =400 гривен.

Таким образом, запускать в год много партий явно невыгодно, но невыгодно и выпустить всего 2 партии в год — слишком велики затраты на хранение! Где же “золотая середина”, сколько партий в год лучше всего выпускать?

Будем строить модель такой системы. Обозначим через N размер партии и найдем количество партий за год — p = N / n 24000 / N.

Получается, что интервал времени между партиями составляет

T = 12 / P (месяцев), а средний запас изделий на складе — N/2 штук.

Сколько же нам будет стоить выпуск партии в n штук за один раз?

Сосчитать нетрудно — 0.1 · 12 · n / 2 гривен на складские расходы в год и 400P гривен за запуск партий по N штук изделий в каждой.

В общем виде годовые затраты составляют

E = TN / 2 + N / n {3 - 2}

Где T = 12 — полное время наблюдения в месяцах.

Перед нами типичная Вариационная задача: найти такое N0, при котором сумма E достигает минимума.

Решение этой задачи найти совсем просто — надо взять производную по N и приравнять эту производную нулю. Это дает

N0 = 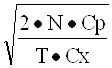, {3 - 3}

Что для нашего примера составляет 4000 единиц в одной партии и соответствует интервалу выпуска партий величиной в 2 месяца.

Затраты при этом минимальны и определяются как

E0 = , {3 - 4}

Что для нашего примера составляет 4800 гривен в год.

Сопоставим эту сумму с затратами при выпуске 2000 изделий в партии или выпуске партии один раз в месяц (в духе недобрых традиций социалистического планового хозяйства):

E1 = 0.1·12·2000/2 + 400·24000/ 2000 = 6000 гривен в год.

Комментарии, как говорится, — излишни!

Конечно, так просто решать задачи выработки оптимальных стратегий удается далеко не всегда, даже если речь идет о Детерминированных данных для описания жизни системы — ее модели. Существует целый класс задач системного анализа и соответствующих им моделей систем, где речь идет о необходимости минимизировать Одну функции многих переменных следующего типа:

E = a1X1 + a2X2 + ..... anXn {3 - 5}

Где Xi — искомые переменные, Ai — соответствующие им коэффициенты или “Веса переменных” и при этом имеют место Ограничения как на переменные, так и на их веса.

Задачи такого класса достаточно хорошо исследованы в специальном разделе прикладной математики — Линейном программировании. Еще в докомпьютерные времена были разработаны алгоритмы поиска экстремумов таких функций E = f(a, X), которые так и назвали — Целевыми. Эти алгоритмы или приемы используются и сейчас — служат основой для разработки прикладных компьютерных программ системного анализа.

Системный подход к решению практических задач управления экономикой, особенно для задач со многими десятками сотен или даже тысячами переменных привел к появлению специализированных, типовых направлений как в области теории анализа, так и в практике.

Наиболее “старыми” и, следовательно, наиболее обкатанными являются методы решения специфичных задач, которые давно уже можно называть Классическими.

Специалистам в области делового администрирования надо знать эти задачи хотя бы на уровне постановки и, главное, в плане моделирования соответствующих систем.

· Задачи управления запасами

Первые задачи управления запасами были рассмотрены еще в 1915 году — задолго не только до появления компьютеров, но и до употребления термина “кибернетика”. Был обоснован метод решения простейшей задачи — минимизация затрат на Заказ и хранение запасов при заданном Спросе на данную продукцию и фиксированном Уровне цен. Решение — размер оптимальной партии обеспечивало наименьшие суммарные затраты за заданный период времени.

Несколько позже были построены алгоритмы решения задачи управления запасами при более сложных условиях — изменении уровня цен (наличие “скидок за качество” и / или “скидок за количество”); необходимости Учета линейных ограничений на складские мощности и т. п.

· Задачи распределения ресурсов

В этих задачах объектом анализа являются системы, в которых приходится выполнять несколько операций с продукцией (при наличии нескольких способов выполнения этих операций) и, кроме того, не хватает ресурсов или оборудования для выполнения всех этих операций.

Цель системного анализа — найти способ наиболее эффективного Выполнения операций с учетом Ограничений на ресурсы.

Объединяет все такие задачи метод их решения — метод математического программирования, в частности, — Линейного программирования. В самом общем виде задача линейного программирования формулируется так:

Требуется обеспечить минимум выражения (целевой функции)

E(X) = C1X1 + C2X2 + ......+ CiXi + ... CnXn {3 - 6} при следующих условиях:

Все Xi положительны и, кроме того, на все Xi налагаются M Ограничений (m < n)

A11·X1 + A12·X2 + ......+ Aij·Xj + ... A1n·Xn = B1;

.....................................................................................

Ai1·X1 + Ai2·X2 + ......+ Aij·Xj + ... Ain·Xn = Bi; {3 - 7}

.....................................................................................

Am1·X1 + Am2·X2 + .....+ Amj·Xj+ ... Amn·Xn = Bm.

Начала теоретического обоснования и разработки практических методов решения задач линейного программирования были положены Д. Данцигом (по другой версии — Л. В.Канторовичем).

Для большинства конкретных приложений универсальным считается т. н. Симплекс-метод поиска цели, для него и смежных методов разработаны специальные пакеты прикладных программ (ППП) для компьютеров.

< Предыдущая		Следующая >