34.07. П7. Задания по теме Нелинейное программирование"
7.1. Дана задача с линейной целевой функцией и нелинейной системой ограничений.
Используя графический метод, найти глобальные экстремумы функции, при этом с 1-го по 5-й вариант выполнения работ принять математическую модель задачи вида
![]()
При ограничениях:
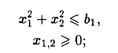
С 6-го по 10-й вариант — вида
![]()
При ограничениях:
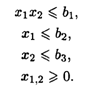
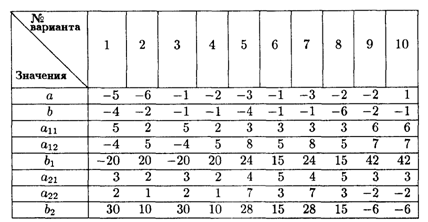
Значения коэффициентов целевых функций и систем ограничений
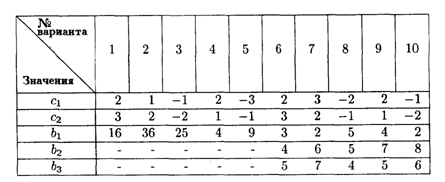
7.2. Дана задача с нелинейной целевой функцией и линейной системой ограничений.
Используя графический метод, найти глобальные экстремумы функции
![]()
При ограничениях:
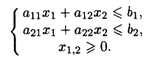
Значения коэффициентов целевой функции и системы ограничений
7.3. Дана задача с нелинейной целевой функцией и нелинейной системой ограничений.
Используя графический метод, найти глобальные экстремумы функции, при этом с 1-го по 5-й вариант выполнения работ принять математическую модель задачи вида
![]()
При ограничениях:
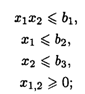
С 6-го по 10-й вариант — вида
![]()
При ограничениях:
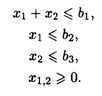
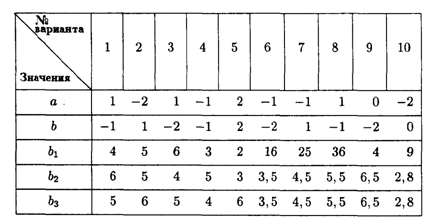
Значения коэффициентов целевой функции и системы ограничений
7.4. Решить задачу дробно-линейного программирования.
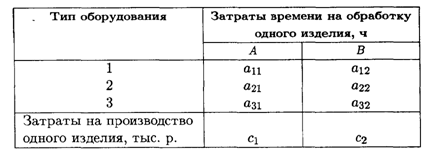
Для производства двух изделий A И В предприятие использует три типа технологического оборудования. Каждое из изделий должно пройти обработку на данном типе оборудования. Время обработки каждого из изделий, затраты, связанные с производством одного изделия, даны в таблице.
Оборудование 1-го и 3-го типов предприятие может использовать не менее B1 и B3 ч соответственно, оборудование 2-го типа — не более B2 ч.
Определить, сколько изделий следует изготовить предприятию, чтобы средняя себестоимость одного изделия была минимальной.
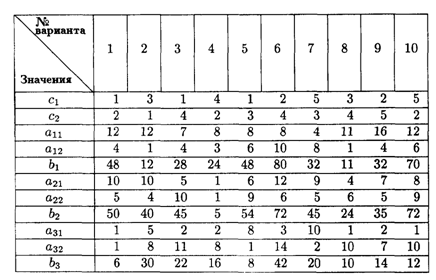
Значения коэффициентов условия задачи
7.5. Дана задача нелинейного программирования
![]()
При ограничении
![]()
Найти условный экстремум с использованием метода множителей Лагранжа.
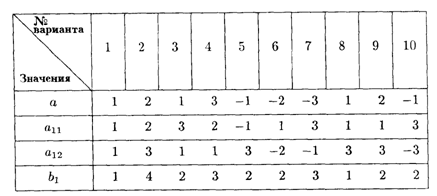
Значения коэффициентов целевой функции и системы ограничений
| < Предыдущая | Следующая > |
|---|