26.3. Планирование загрузки оборудования с учетом максимальной производительности станков
Рассмотрим следующую задачу.
На предприятии пять станков различных видов, каждый из которых может выполнять пять различных операций по обработке деталей. Известна производительность каждого станка при выполнении каждой операции, заданная матрицей
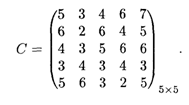
Определить, какую операцию и за каким станком следует закрепить, чтобы суммарная производительность была максимальной при условии, что за каждым станком закреплена только одна операция.
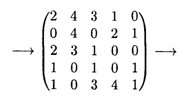
Решение. Так как в задаче требуется определить max, a алгоритм метода дан для задач на min, умножим матрицу С на (—1). Сложим полученную матрицу, имеющую отрицательные коэффициенты, с положительным числом, например с числом 10. Получим

Минимальные элементы в строчках есть 3, 4, 4, 6, 4. Вычтем их из соответствующих элементов матрицы, получим
Так как назначение не получено, вычеркиваем строку 2, столбцы 2, 4, 5:
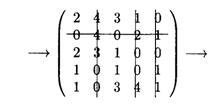
Минимальный элемент равен 1. Вычитаем его из всех невычеркнутых элементов и складываем со всеми элементами, расположенными на пересечении двух линий. Получаем
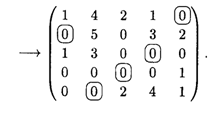
Оптимальное решение, соответствующее последней матрице, равно
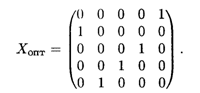
Суммарная производительность: 6 + 6 + 3 + 6 + 7= 28.
Таким образом, на первом станке надо делать 5-ю операцию, на втором — 1-ю операцию, на третьем — 4-ю операцию, на четвертом — 3-ю операцию, на пятом станке — 2-ю операцию. Суммарная производительность: 28 деталей в единицу времени.
| < Предыдущая | Следующая > |
|---|