25.6. Упражнения
Решить следующие задачи параметрического программирования с параметром в целевой функции.
25.1. L(![]() ) = -λX1 — х2 → Min, 1 ≤ λ ≤ 11 при ограничениях:
) = -λX1 — х2 → Min, 1 ≤ λ ≤ 11 при ограничениях:
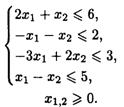
25.2. L(![]() ) = 5X1 + (2 + 3λ)X2 → max, 0 ≤ λ ≤ 10 при ограничениях:
) = 5X1 + (2 + 3λ)X2 → max, 0 ≤ λ ≤ 10 при ограничениях:
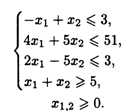
25.3. L(![]() ) = 2X1 + (3 + 4λ)X2 → max, -
) = 2X1 + (3 + 4λ)X2 → max, -![]() < λ <
< λ < ![]() при ограничениях:
при ограничениях:
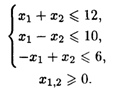
25.4. L(![]() ) = (1 + λ)X1 + (2 - λ)X2 → min, -1 ≤ λ ≤ 4 при ограничениях:
) = (1 + λ)X1 + (2 - λ)X2 → min, -1 ≤ λ ≤ 4 при ограничениях:
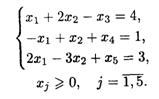
25.5. L(![]() ) = (3 + 3λ)X1 + 2X2 + (5 – 6λ)X3 → max, -
) = (3 + 3λ)X1 + 2X2 + (5 – 6λ)X3 → max, -![]() < λ <
< λ < ![]() при ограничениях:
при ограничениях:
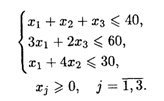
Решить следующие транспортные параметрические задачи.
25.6. Произвести транспортировку однородного груза с трех складов с объемами хранения 100, 200, 200 т соответственно пяти оптовым рынкам с потребностями 80, 70, 100, 150, 100 т соответственно. Стоимость транспортных расходов задана матрицей
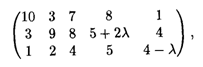
Причем стоимость перевозки груза со второго склада на четвертый рынок и с третьего склада на пятый рынок изменяется в некотором диапазоне 0 ≤ λ ≤ 2.
Определить план перевозок, обеспечивающий минимальные транспортные расходы в заданном диапазоне изменения параметра λ.
25.7. Имеются четыре поставщика однородного груза с объемами поставок 100, 70, 70, 20 т и три потребителя с объемами потребления 120, 80, 60 т. Cтоимость транспортных расходов задана матрицей
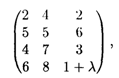
Причем стоимость перевозки груза от четвертого поставщика до третьего потребителя изменяется в диапазоне 0 ≤ λ ≤ 9.
Определить оптимальный план перевозок, обеспечивающий минимальные транспортные расходы.
| < Предыдущая | Следующая > |
|---|