22.6. Упражнения
Для следующих задач составить математические модели двойственных задач и по решению исходной найти оптимальное решение двойственной.
22.1. L(![]() ) = X1 + 3X3 + 3X4 → Min при ограничениях:
) = X1 + 3X3 + 3X4 → Min при ограничениях:
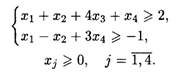
22.2. L(![]() ) = 2Х1 + х2 – 3X3 + Х4 → max при ограничениях:
) = 2Х1 + х2 – 3X3 + Х4 → max при ограничениях:
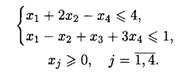
22.3. L(![]() ) = - х1 + X2 + 6X3 — х4 → min при ограничениях:
) = - х1 + X2 + 6X3 — х4 → min при ограничениях:
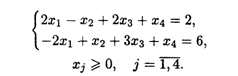
22.4. L(![]() ) = -3X2 + Х3 – х4 → max при ограничениях:
) = -3X2 + Х3 – х4 → max при ограничениях:
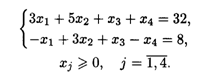
22.5. L(![]() ) = -3X1 + X2+ 3X3 – 4X4 → min при ограничениях:
) = -3X1 + X2+ 3X3 – 4X4 → min при ограничениях:
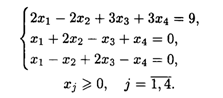
Составить математическую модель двойственных задач и по ее решению найти оптимальное решение исходной.
22.6. L(![]() ) = l,5X1 + 2Х2 → max при ограничениях:
) = l,5X1 + 2Х2 → max при ограничениях:
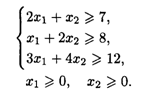
22.7. L(![]() ) = X1 - 2X2 + X4 → min При ограничениях:
) = X1 - 2X2 + X4 → min При ограничениях:
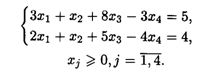
22.8. L(![]() ) = -2X1 + х2 → min при ограничениях:
) = -2X1 + х2 → min при ограничениях:
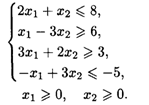
22.9. Для производства трех изделий А, В и С используются три вида сырья. Каждый из них используется в объеме, не превышающем 180, 210 и 236 кг. Нормы затрат каждого из видов сырья на одно изделие и цена единицы изделий приведены в табл. 22.4.

Определить план выпуска изделий, обеспечивающий получение максимального дохода.
Составить для данной задачи двойственную и найти:
1) оптимальный план двойственной задачи;
2) интервалы устойчивости двойственных оценок;
3) увеличение максимального дохода при увеличении количества сырья 2-го и 3-го видов на 80 и 160 кг соответственно и при уменьшении количества сырья 1-го вида на 40 кг. Оценить раздельное и суммарное влияние этих изменений;
4) целесообразность введения в план производства 4-го изделия, нормы затрат сырья на одно изделие которого составляют 2, 4 и 6 кг, а цена изделия равна 18 усл. ед.;
5) оптимальные планы исходной и двойственной задач, если количество сырья 1, 2 и 3 равно 140, 250 и 240 кг соответственно.
| < Предыдущая | Следующая > |
|---|