22.4. Экономический анализ задач с использованием теории двойственности
Рассмотрим задачу оптимального использования ресурсов, запишем ее математическую модель

При ограничениях:
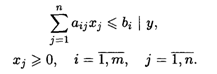
Двойственная задача имеет вид
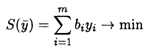
При ограничениях:
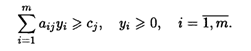
ТЕОРЕМА 3. Значения переменных уi в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов системы ограничений исходной задачи на оптимальное значение ее целевой функции, т. е.
![]()
Примем ![]() Li ≈ ΔLi,
Li ≈ ΔLi, ![]() Bi ≈ Δbi, тогда ΔLi ≈ Yi • Δbi.
Bi ≈ Δbi, тогда ΔLi ≈ Yi • Δbi.
Для задачи оптимального использования сырья это уравнение показывает, что при изменении I-го ресурса оптимальный доход является линейной функцией от его приращения, причем коэффициентом служит Уi — i-я компонента оптимального решения двойственной задачи.
Если Yi мало, то значительному увеличению I-го ресурса будет соответствовать небольшое увеличение оптимального дохода и ценность ресурса невелика.
Если Yi = 0, то при увеличении I-го ресурса оптимальный доход остается неизменным и ценность этого ресурса равна нулю. В самом деле, сырье, запасы которого превышают потребности в нем, не представляет ценности для производства и его оценку можно принять за нуль.
Если Уi велико, то незначительному увеличению I-го ресурса будет соответствовать существенное увеличение оптимального дохода и ценность ресурса высока. Уменьшение ресурса ведет к существенному сокращению выпуска продукции.
Переменную Уi считают некоторой характеристикой ценности I-го ресурса. В частности, при увеличении I-го ресурса на единицу (Δbi = 1) оптимальный доход возрастает на Yi, что позволяет рассматривать Yi как "условную цену", оценку единицы I-го ресурса, объективно обусловленную оценку.
Так как УI представляет частную производную от оптимального дохода по I-му ресурсу, то Уi характеризует скорость изменения оптимального дохода при изменении I-го ресурса.
С помощью Yi можно определить степень влияния ограничений на значение целевой функции. Предельные значения (нижняя и верхняя границы) ограничений ресурсов, для которых Yi остаются неизменными, определяются по формулам:
![]()
Где Xj — значение переменной в оптимальном решении; Dij — Элементы матрицы (dij) = А-1, обратной к матрице базиса оптимального решения, для которой А = (Aij)MXN.
Если в план включаются новые виды продукции, то их оценка находится по формуле
![]()
Если ΔJ < 0, то новый вид продукции улучшает план. При ΔJ > 0 нецелесообразно включать новый вид продукции.
| < Предыдущая | Следующая > |
|---|