18.6.5. Статистические оценки параметров распределения
Значения количественного признака Х1, х2, ..., Хk в выборке можно рассматривать как независимые случайные величины. В таком случае нахождение статистической оценки неизвестного параметра теоретического распределения означает отыскание функции от наблюдаемых случайных величин, которая и даст нам приближенное значение искомого параметра. Укажем виды статистических оценок.
Несмещенной называется статистическая оценка ![]() , математическое ожидание которой равно оцениваемому параметру
, математическое ожидание которой равно оцениваемому параметру ![]() при любой выборке:
при любой выборке:
![]()
Смещенной называется оценка, при которой условие (18.51) не выполнено. Эффективной называется оценка, которая имеет минимальную дисперсию при заданном объеме выборки П. Состоятельной называется статистическая оценка типа (18.50), которая при П > ![]() стремится по вероятности к оцениваемому параметру.
стремится по вероятности к оцениваемому параметру.
Теперь укажем виды числовых характеристик оценок. Прежде всего, это средние. Генеральная средняя для изучаемого количественного признака Х по генеральной совокупности
![]()
И Выборочная средняя
![]()
Если значения признака Х1, X2, …, Хk в выборке имеют соответственно частоты N1, N2, ..., Nk, то последнюю формулу можно переписать в виде
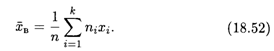
Можно показать, что выборочная средняя (18.52) является несмещенной оценкой; это аналог математического ожидания случайной величины.
Введем в рассмотрение величины, характеризующие отклонение значений количественного признака Х от своего среднего значения. Это Генеральная дисперсия:
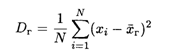
И выборочная дисперсия:
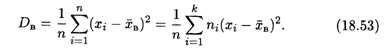
Можно показать, что для вычисления этих характеристик справедливы более удобные формулы, аналогичные дисперсии случайной величины; так, формула (18.53) принимает вид
![]()
Генеральное среднее квадратическое отклонение определяется как
![]()
Аналогично вводится и Выборочное среднее квадратическое отклонение
![]()
Пример 4. Выборка задана таблицей распределения

Найти выборочные характеристики: среднюю, дисперсию и среднее квадратическое отклонение.
Решение. По формуле (18.52) сначала находим ![]() В:
В:
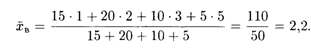
Затем по формулам (18.54) и (18.55) находим две другие искомые величины:
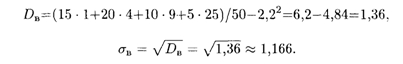
| < Предыдущая | Следующая > |
|---|