18.2.2. Дисперсия дискретной случайной величины
Как уже говорилось выше, математическое ожидание является средней характеристикой случайной величины. Однако оно не характеризует случайную величину достаточно полно, и по этой причине рассматриваются и другие числовые характеристики. Пусть Х — случайная величина, а М(Х) — ее математическое ожидание.
Определение 2. Разность между случайной величиной и ее математическим ожиданием называется Отклонением.
Пусть закон распределения случайной величины Х дается формулой (18.1), тогда отклонение X - M(X) имеет следующий закон распределения:
![]()
Отклонение имеет важное свойство, которое устанавливается непосредственно из свойств математического ожидания:
![]()
Т. е. математическое ожидание отклонения равно нулю.
Пример 5. По данным примера 3 найти закон распределения отклонения числа проданных за день автомашин.
Решение. Как было подсчитано в примере 3, М(Х) = 2,675. Тогда, согласно (18.8), искомый закон определяется следующей таблицей:

На практике важной характеристикой является рассеяние возможных значений случайной величины вокруг ее среднего значения. Среднее значение отклонения, согласно (18.9), равно нулю, так как суммируются отрицательные и положительные отклонения (см. пример 5), поэтому целесообразно ввести в рассмотрение абсолютные значения отклонений или их квадраты.
Определение 3. Математическое ожидание квадрата отклонения называется Дисперсией, или Рассеянием:
![]()
Пусть случайная величина задана законом распределения (18.1), тогда квадрат отклонения этой случайной величины имеет следующий закон распределения:
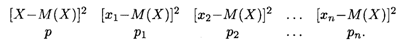
Отсюда, согласно формуле (18.10), получаем формулу дисперсии в развернутом виде:
![]()
При вычислении дисперсии часто бывает удобно воспользоваться формулой, которая непосредственно выводится из формулы (18.10):
![]()
Пример 6. Найти дисперсию ежедневной продажи числа автомашин по данным примера 3.
Решение. Закон распределения случайной величины X2 имеет вид

Математическое ожидание М(Х2) подсчитывается из этой таблицы:
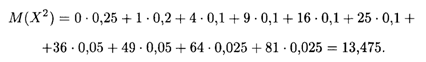
Математическое ожидание М(Х) = 2,675. Следовательно, согласно формуле (18.11), получаем искомую величину дисперсии:
![]()
| < Предыдущая | Следующая > |
|---|