17.4. Обобщения теорем сложения и умножения. Появление только одного из независимых событий
Рассмотрим примеры совместного применения теорем сложения и умножения. Пусть два независимых события А1 и А2 имеют вероятности появления соответственно P1 и Р2. Найдем вероятность появления только одного из этих событий. Для этого введем новые события: В1 и B2. Событие В1 состоит в том, что событие А1 наступило, а событие А2 не наступило; иными словами, В1 = A1![]() 2. Аналогичным образом определяется и событие B2 =
2. Аналогичным образом определяется и событие B2 = ![]() 1A2 (совместное ненаступление события A1 и наступление события А2). Поскольку события А1 и A2 независимы, то независимы также и противоположные coбытия
1A2 (совместное ненаступление события A1 и наступление события А2). Поскольку события А1 и A2 независимы, то независимы также и противоположные coбытия ![]() 1 и
1 и ![]() 2; тогда события В1 и В2 являются несовместными. Вероятность наступления только одного из событий А1 и А2 находится как сумма вероятностей несовместных событий В1 и B2:
2; тогда события В1 и В2 являются несовместными. Вероятность наступления только одного из событий А1 и А2 находится как сумма вероятностей несовместных событий В1 и B2:
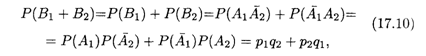
Где q1 = 1 – P1 , Q2 = 1 - Р2.
Аналогичным образом можно убедиться в справедливости формулы вероятности наступления только одного из трех независимых событий A1, А2, А3 с вероятностями наступления соответственно Р1, р2 и р3:
![]()
Где Bi — произведения наступившего события АI и двух других ненаступивших событий (I = 1, 2, 3). Для случая П независимых событий формула вероятности наступления только одного из них имеет аналогичный вид — сумма П слагаемых, каждый член которой представляет собой произведение вероятности наступления одного из событий на вероятности (N - 1) других противоположных событий.
Пример 1. Предприниматель решил вложить свои средства поровну в два контракта, каждый из которых принесет ему прибыль в размере 100%. Вероятность того, что любой из контрактов не "лопнет", равна 0,8. Какова вероятность того, что по истечении контрактов предприниматель по меньшей мере ничего не потеряет?
Решение. Предприниматель по крайней мере ничего не потеряет, если либо не "лопнет" один из контрактов (другой возместит ему потери), либо будут выполнены оба контракта. Пусть события А1 и А2 — это выполнение соответствующих контрактов (вероятность Р = 0,8); эти события являются независимыми. Противоположные им события ![]() 1 и
1 и ![]() 2 — невыполнение контрактов (вероятность Q = 0,2). Тогда события В1 = А1
2 — невыполнение контрактов (вероятность Q = 0,2). Тогда события В1 = А1![]() 2, В2 =
2, В2 = ![]() 1A2 и A1A2 являются несовместными (последнее событие — это выполнение обоих контрактов). Искомая вероятность определяется с учетом формул (17.10) и (17.7):
1A2 и A1A2 являются несовместными (последнее событие — это выполнение обоих контрактов). Искомая вероятность определяется с учетом формул (17.10) и (17.7):
![]()
| < Предыдущая | Следующая > |
|---|