17.3. Теорема умножения вероятностей. Произведение событий и условная вероятность
Определение 1. Произведением двух событий А и В называется событие АВ, означающее совместное появление этих событий (см. гл. 1.1, произведение множеств).
Например, если событие А — шар, событие В — белый цвет, то их произведение АВ — белый шар. Аналогично определяется произведение Нескольких событий, как совместное появление их всех.
Если при вычислении вероятности события никаких других ограничений кроме необходимого комплекса условий S не налагается, то такая вероятность называется Безусловной. Если же налагаются другие дополнительные условия, содержащие случайные события, то вероятность такого события называется Условной.
Определение 2. Вероятность события В в предположении о наличии события А называют условной вероятностью РA(В).
Пример 1. В ящике лежит 11 деталей, 3 из них нестандартные. Из ящика дважды берут по одной детали, не возвращая их обратно. Найти вероятность того, что во второй раз из ящика будет извлечена стандартная деталь — событие В, если в первый раз была извлечена нестандартная деталь — событие А.
Решение. После первого извлечения в ящике из 10 деталей осталось 8 стандартных, и, следовательно, искомая вероятность
![]()
Пусть теперь известны вероятность Р(А) события А и условная вероятность РА(В) события В. Тогда справедлива следующая теорема.
ТЕОРЕМА 3. Вероятность произведения двух событий определяется формулой
![]()
Пример 2. В условиях примера 1 найти вероятности того, что в первый раз извлечена нестандартная деталь, а во второй раз — стандартная, и наоборот.
Решение. Итак, событие А — это извлечение из ящика нестандартной детали, а событие В — стандартной. Тогда возможны два случая. 1) Вероятность Р(А) = 3/11, а условная вероятность РA(В) = 0,8. Искомая вероятность произведения этих событий (их совместного появления в указанном порядке) равна, согласно теореме 17.3,
![]()
2) Вероятность Р(В) = 8/11, а условная вероятность РB(А) = 0,3. Мы видим, что и в этом случае вероятность произведения событий Р(ВА) = Р(В)РB(А) ≈ 0,22.
В этом примере мы проверили известное в теории равенство
![]()
Теорема 17.3 допускает обобщение на случай произведения любого числа событий A1, А2, А3, ..., An:
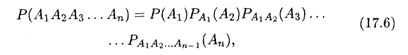
Т. е. вероятность совместного появления П событий равна произведению П вероятностей, где PA1A2...Ak-1(Ak) — условные вероятности событий Ak в предположении, что события A1A2 ... Ak-1 уже произошли (K = 1, 2, ... , П).
Пример 3. В урне находится 4 белых шара, 5 красных и 3 синих. Наудачу извлекают по одному шару, не возвращая его обратно. Найти вероятность того, что в первый раз появится белый шар (событие А), во второй раз — красный (событие В), в третий — синий (событие С).
Решение. Вероятность появления белого шара в первом извлечении Р(А) = 1/3; условная вероятность появления красного шара во втором извлечении при условии появления в первый раз белого шара РA(В) = 5/11; условная вероятность появления синего шара в третьем извлечении при условиях появления в предыдущих извлечениях белого и красного шаров РAB(С) = 0,3. Искомая вероятность определяется по формуле (17.6) при П = 3:
![]()
| < Предыдущая | Следующая > |
|---|