17.1. Основные понятия теории вероятностей

Некоторые формулы комбинаторики

Пусть задано конечное множество элементов некоторой природы. Из них можно составлять определенные комбина­ции, количества которых изучает комбинаторика. Некоторые ее формулы используются в теории вероятности; приведем их.

Комбинации, состоящие из одной и той же совокупности П различных элементов и отличающиеся только порядком их расположения, называются Перестановками. Число всех воз­можных перестановок определяется произведением чисел от единицы до П:

Пример 1. Сколько четырехзначных чисел можно составить из цифр 1, 2, 3 и 4 с использованием всех указанных цифр в каждом числе?

Решение. Искомое число равно Р4 = 4! = 1 ∙ 2 ∙ 3 ∙ 4 = 24.

Комбинации по Т элементов, составленные из П различных элементов (M ≤ П), отличающиеся друг от друга либо эле­ментами, либо их порядком, называются Размещениями. Число всевозможных размещений

Пример 2. Сколько трехзначных чисел можно составить из семи различных цифр при отсутствии среди них нуля?

Решение. Искомое количество цифр

Комбинации, содержащие по Т элементов каждая, состав­ленные из П различных элементов (M ≤ П) и различающиеся хотя бы одним элементом, называются Сочетаниями. Число сочетаний дается формулой

Можно показать, что справедливы формулы

В частности, первую из формул удобно использовать в расче­тах, когда Т > П/2.

Напомним формулу бинома Ньютона, в которой участвуют коэффициенты (17.1):

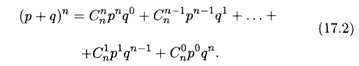
Пример 3. Сколькими способами можно выбрать а) по три карты, б) по 32 карты из колоды, содержащей 36 игральных карт?

Решение. Искомое число способов:

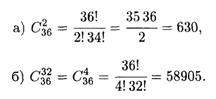
< Предыдущая		Следующая >