04.2.1. Понятие дифференциала функции. Определение и геометрический смысл дифференциала
Определение 1. Дифференциалом функции у = F(X) в точке X0 называется главная линейная относительно ΔX часть приращения функции в этой точке:
![]()
Дифференциалом Dx независимой переменной Х будем называть приращение этой переменной ΔX, т. е. соотношение (4.3) принимает вид
![]()
Из равенства (4.4) производную F'(X) в любой точке Х можно вычислить как отношение дифференциала функции Dy к дифференциалу независимой переменной Dx:
![]()
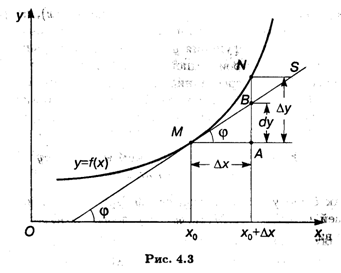
Дифференциал функции имеет четкий геометрический смысл (рис. 4.3). Пусть точка М на графике функции У = F{X) соответствует значению аргумента X0, точка N — значению аргумента X0 + ΔX, MS — касательная к кривой F(X) в точке М, φ — угол между касательной и осью Ох. Тогда МА — приращение аргумента, AN — соответствующее приращение функции. Рассматривая треугольник АВМ, получаем, что АВ = ΔX tg φ = F'(X0) ΔX = Dy, т. е. это главная по порядку величины ΔX и линейная относительно нее часть приращения функции ΔУ. Оставшаяся часть более высокого порядка малости соответствует отрезку BN.
| < Предыдущая | Следующая > |
|---|