4.6.2 Связность. Связные компоненты графа

В неориентированном графе G две вершины А И B называются Связанными, если существует какой-либо маршрут с концами А И B. Если этот маршрут проходит через какую-то вершину Ai более одного раза, то можно, очевидно, удалить его циклический участок, и при этом остающиеся ребра будут составлять маршрут, связывающий вершины А И B. Отсюда следует, что вершины, связанные маршрутом, всегда связаны простой цепью. Если любая пара вершин в графе связана, то граф называется Связанным.

Пусть G – связанный неориентированный граф. Длина маршрута между двумя вершинами в нем равна, очевидно, количеству ребер, соединяющих эти две вершины. Так как связанные вершины всегда можно связать простой цепью, то существует набор простых цепей S (A, B) с концами в А и B. Длины этих простых цепей выражаются неотрицательными целыми числами. Следовательно, между А и B должна существовать простая цепь наименьшей длины. Эта наименьшая длина называется Расстоянием Между вершинами А и B И обозначается D(A, B). По определению D(A, А) = 0; если А и B не связаны, то D(A, B) = .

В связанном графе расстояние является метрикой и удовлетворяет следующим аксиомам (аксиомы метрики):

1) D(A, B) ³ 0 и D(A, B) = 0, тогда, когда А = B;

2) D(A, B) = D(B, А);

3) D(A, B) + D(B, С) ³ D(A, С).

Диаметром Графа G называют длину максимальной из кратчайших простых цепей. Обозначают D(G).

Например: Для графа G диаметр D(G) = 2 (рис. 4.11).

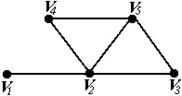
Рис. 4.11 – Пример нахождения диаметра графа

< Предыдущая