01. Задача о диете (упрощенный вариант)

Предположим для определенности, что необходимо составить самый дешевый рацион питания цыплят, содержащий необходимое количество определенных питательных веществ (для простоты, тиамина Т и ниацина Н).

Таблица 8.1

Исходные данные в задаче об оптимизации смеси

	Содержание в 1 унции К	Содержание в 1 унции С	Потребность
Вещество Т	0,10 мг	0,25 мг	1,00 мг
Вещество Н	1,00 мг	0,25 мг	5,00 мг
Калории	110,00	120,00	400,00
Стоимость 1 унции, в центах	3,8	4,2

Пищевая ценность рациона (в калориях) должна быть не менее заданной. Пусть для простоты смесь для цыплят изготавливается из двух продуктов - К и С. Известно содержание тиамина и ниацина в этих продуктах, а также питательная ценность К и С (в калориях). Сколько К и С надо взять для одной порции куриного корма, чтобы цыплята получили необходимую им дозу веществ Н и Т и калорий (или больше), а стоимость порции была минимальна? Исходные данные для расчетов приведены в Табл. 8.1.

Задача линейного программирования имеет вид:

3,8K+4,2Cð min

0,10K+0,25C≥1,00

1,00K+0,25C≥5,00

110K+120C≥400,00

K≥0

C≥0

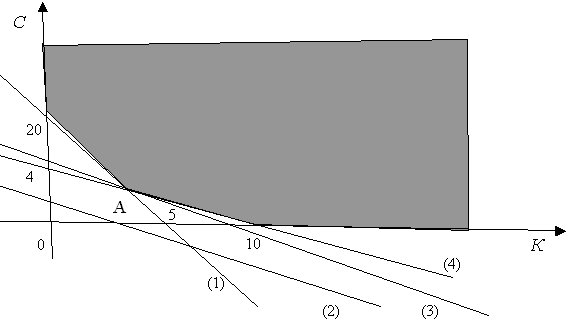
Ее графическое решение представлено на Рис. 8.1

Рис. 8.41. Графическое решение задачи об оптимизации смеси

На рис. 8.4 ради облегчения восприятия четыре прямые обозначены номерами (1) - (4). Прямая (1) описывается уравнением 1,00K+0,25C=5,00 (ограничение по веществу Н). Она проходит, как и показано на рисунке, через точки (5, 0) на оси абсцисс и (0, 20) на оси ординат. Обратите внимание, что допустимые значения параметров (К, С) лежат выше прямой (1) или на ней, в отличие от ранее рассмотренных случаев в предыдущей производственной задаче линейного программирования.

Прямая (2) - это прямая 110K+120C=400,00 (ограничение по калориям). Обратим внимание, что в области неотрицательных С она расположена всюду ниже прямой (1). Действительно, это верно при K=0, прямая (1) проходит через точку (0, 20), а прямая (2) - через расположенную ниже точку (0, 400/120). Точка пересечения двух прямых находится при решении системы уравнений

1,00K+0,25C=5,00

110K+120C=400,00

Из первого уравнения K=5-0,25C. Подставим во второе:
110(5-0,25C)+120C=400, откуда 550-27,5C+120C=400. Следовательно, 150=-92,5C , т. е. решение достигается при отрицательном С. Это и означает, что при всех положительных С прямая (2) лежит ниже прямой (1). Значит, если выполнено ограничение по Н, то обязательно выполнено и ограничение по калориям. Мы столкнулись с новым явлением - некоторые ограничения с математической точки зрения могут оказаться лишними. С экономической точки зрения они необходимы, отражают существенные черты постановки задачи, но в данном случае внутренняя структура задачи оказалась такова, что ограничение по калориям не участвует в формировании допустимой области параметров и нахождении решения.

Прямая (4) - это прямая 0,1K+0,25C=1 (ограничение по веществу Т). Она проходит, как и показано на рисунке, через точки (10, 0) на оси абсцисс и (0, 4) на оси ординат. Обратите внимание, что допустимые значения параметров (К, С) лежат выше прямой (4) или на ней, как и для прямой (1).

Следовательно, область допустимых значений параметров (К, С) является неограниченной сверху. Из всей плоскости она выделяется осями координат (лежит в первом квадранте) и прямыми (1) и (4) (лежит выше этих прямых, а также включает граничные отрезки). Область допустимых значений параметров, т. е. точек (К, С), можно назвать "неограниченным многоугольником". Минимум целевой функции 3.8K+4,2C может достигаться только в вершинах этого "многоугольника". Вершин всего три. Это пересечения с осями абсцисс (10, 0) и ординат (0, 20) прямых (1) и (4) (в каждом случае из двух пересечений берется то, которое удовлетворяет обоим ограничениям). Третья вершина - это точка А пересечения прямых (1) и (4), координаты которой находятся при решении системы уравнений

0,10K+0,25C=1,00

1,00K+0,25C=5,00

Из второго уравнения K=5-0,25C, из первого
0,1(5-0,25C)+0,25C=5,00=0,25C=0,5+0,225C=1, откуда C=0,5/0,225=20/9 и K=5-5/9=40/9. Итак, A=(20/9,40/9).

Прямая (3) на Рис. 8.5 - это прямая, соответствующая целевой функции 3,8K+4,2C. Она проходит между прямыми (1) и (4), задающими ограничения, и минимум достигается в точке А, через которую и проходит прямая (3). Следовательно, минимум равен 3,8X40/9+4,2X20/9=236/9. Задача об оптимизации смеси полностью решена.

Двойственная задача, построенная по ранее описанным правилам, имеет приведенный ниже вид (мы повторяем здесь и исходную задачу об оптимизации смеси, чтобы наглядно продемонстрировать технологию построения двойственной задачи):

3,8K+4,2Cð min W1+5W2+400W3ð max

0,10K+0,25C ≥1,00 0,1W1+1,10W2+110W3≤3,8

1,00K+0,25C ≥5,00 0,25W1+0,25W2+120W3≤4,2

110K+120C ≥400,00 W1≥0

K ≥0 W2≥0

C ≥0 W3≥0

Минимальное значение в прямой задаче, как и должно быть, равно максимальному значению в двойственной задаче, т. е. оба числа равны 236/9. Интерпретация двойственных переменных: W1 - "стоимость" единицы вещества Т, а W2 - "стоимость" единицы вещества Н, измеренные "по их вкладу" в целевую функцию. При этом W3=0, поскольку ограничение на число калорий никак не участвует в формировании оптимального решения. Итак, W1,W2,W3 - это т. н. объективно обусловленные оценки (по Л. В. Канторовичу) ресурсов (веществ Т и Н, калорий).

Следующая >