22. Застосування операційного числення до задач електротехніки
Методи операційного числення дозволяють розраховувати будь-які процеси в складних електричних ланцюгах при довільній зовнішній напрузі. Ці методи заклав в електротехніку англійський інженер-електрик О. Хевісайд.
Розглянемо простіший випадок: коливальний контур. Як відомо, диференціальне рівняння для струму ![]() у коливальному контурі (рис. 26) має вигляд:
у коливальному контурі (рис. 26) має вигляд:
 , (34)
, (34)
Де ![]() –опір,
–опір, ![]() –індуктивність,
–індуктивність, ![]() –електродвижуча сила.
–електродвижуча сила.
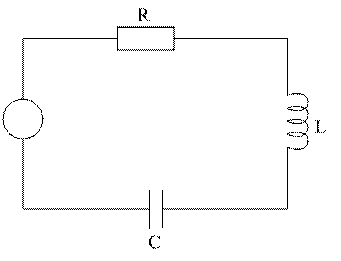
Рис. 26
Будемо вважати, що в початковий момент струм дорівнює нулю: ![]() . Останній член лівої частини рівняння є напруга на обкладках конденсатора; його вираз показує, що при
. Останній член лівої частини рівняння є напруга на обкладках конденсатора; його вираз показує, що при ![]() ця напруга дорівнює нулю, тобто в початковий момент заряди на обкладках конденсатора відсутні. Ці початкові умови відповідають задачам вмикання.
ця напруга дорівнює нулю, тобто в початковий момент заряди на обкладках конденсатора відсутні. Ці початкові умови відповідають задачам вмикання.
Введемо операторний струм ![]() і операторну напругу
і операторну напругу ![]() . За теоремою диференціювання оригіналу
. За теоремою диференціювання оригіналу 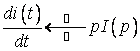 , тому що
, тому що ![]() , а за теоремою інтегрування
, а за теоремою інтегрування  . Рівняння коливального контуру перепишемо в операторному вигляді:
. Рівняння коливального контуру перепишемо в операторному вигляді:
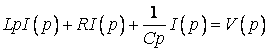 ,
,
Звідки
 (35),
(35),
де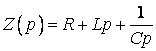 –операторний опір контуру.
–операторний опір контуру.
Формула (35) називається операторною формою закону Ома.
За знайденим операторним струмом ![]() , застосовуючи теорему обернення, можна відновити і сам струм:
, застосовуючи теорему обернення, можна відновити і сам струм:
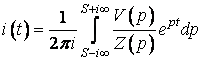
В конкретних задачах можна використовувати таблиці оригіналів та зображень.
Нехай в коливальний контур включається постійний струм: ![]() . Тоді
. Тоді 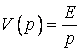 і формула (35) приймає вигляд:
і формула (35) приймає вигляд:
 .
.
Якщо знайти дискримінант виразу ![]() , одержимо:
, одержимо:
1) 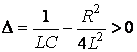 ,
, 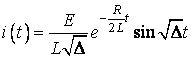 ;
;
2) 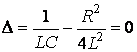 ,
, 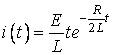 ;
;
3) 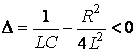 ,
,  .
.
В першому випадку маємо згасаючі гармонічні коливання, в другому та третьому випадках згасаючі аперіодичні процеси. В третьому випадку струм ![]() краще представити в іншому вигляді. Корні тричлена
краще представити в іншому вигляді. Корні тричлена ![]() рівні
рівні 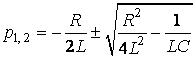 , вони дійсні та від’ємні. Запишемо операторний струм у вигляді:
, вони дійсні та від’ємні. Запишемо операторний струм у вигляді:

Знайдемо оригінал для  .
.
Одержимо
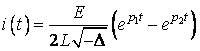 ,
,
Де ![]() і
і ![]() .
.
Звідси видно, що ![]() при
при ![]() .
.
Так же просто розв’язується задача про вмикання в контур синусоїдальної напруги ![]() ( в цьому випадку
( в цьому випадку  ).
).
Зупинимося на ролі інтеграла Дюамеля. Нехай в контур вмикається постійна одинична напруга ![]() . Тоді
. Тоді 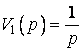 і за формулою (35)
і за формулою (35)
 , або
, або 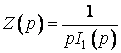 .
.
Якщо тепер в контур включити будь-яку напругу ![]() , то
, то
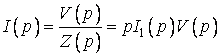 (36)
(36)
За формулою (29)
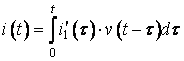
![]() ,
,
Або  .
.
Таким чином, знаючи реакцію контуру на одиничну напругу, ми за допомогою написаних формул зможемо обчислити реакцію контуру на будь-яку зовнішню напругу. В одержані формули не входять ні зображення напруги ![]() , ні, що головне, операторний опір контуру
, ні, що головне, операторний опір контуру ![]() . Останнє означає, що ми можемо розрахувати контур, фактично не знаючи його параметрів, якщо тільки експериментально одержали струм
. Останнє означає, що ми можемо розрахувати контур, фактично не знаючи його параметрів, якщо тільки експериментально одержали струм ![]() –реакцію контуру на одиничну напругу.
–реакцію контуру на одиничну напругу.
Перейдемо до випадку ненульових початкових умов. Будемо вважати, що в початковий момент в контурі є струм ![]() , і що на обкладках конденсатора є початковий заряд
, і що на обкладках конденсатора є початковий заряд ![]() . Остання умова приводить до деякої зміни диференціального рівняння контуру, саме, до падіння напруги на конденсаторі треба додати постійний доданок
. Остання умова приводить до деякої зміни диференціального рівняння контуру, саме, до падіння напруги на конденсаторі треба додати постійний доданок ![]() , і рівняння має вигляд:
, і рівняння має вигляд:
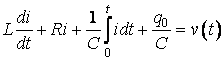
Перейдемо до операторного рівняння і, враховуючи, що тепер ![]() , одержимо
, одержимо
 ,
,
Звідки
 ,
,
де ![]() , а
, а ![]() –операторний опір контуру.
–операторний опір контуру.
Таким чином, до струму, що визначається операторною формулою ![]() , додається ще струм, операторний вираз якого дорівнює
, додається ще струм, операторний вираз якого дорівнює 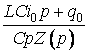 . Цей струм відповідає заданим початковим умовам і зветься струмом короткого замикання. Він одержується, якщо в рівнянні контуру прийняти
. Цей струм відповідає заданим початковим умовам і зветься струмом короткого замикання. Він одержується, якщо в рівнянні контуру прийняти ![]() , тобто накоротко замкнути контур.
, тобто накоротко замкнути контур.
Аудиторне заняття 5. (АЗ-5)
1. Розв’язати рівняння:

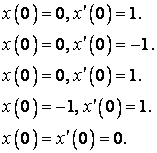
2. Розв’язати систему диференціальних рівнянь:

Самостійна робота.
1. Розв’язати ДР.
2. Розв’язати систему ЛДР.
Варіант 1. ![]() .
.
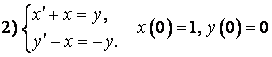 .
.
Варіант 2. ![]() .
.
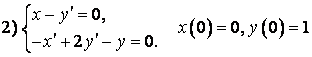 .
.
Варіант 3. ![]() .
.
 .
.
| < Предыдущая | Следующая > |
|---|