20. Розв'язання ЛДР

Одним із важливих застосувань операційного числення, пов’язаних з перетворенням Лапласа, є розв’язання лінійних диференціальних рівнянь з сталими коефіцієнтами.

Розглянемо ЛДР з сталими коефіцієнтами

, (32)

де - дійсні числа.

Будемо вважати, що шукана функція , усі її похідні, а також функція є оригіналами. Потрібно знайти рішення диференціального рівняння (32), що задовольняє початковим умовам:

, (33)

де - задані числа.

Загальна схема розв’язання задачі Коші для ЛДР з сталими коефіцієнтами така:

1) від диференціального рівняння (32) із початковими умовами (33) в просторі оригіналів за допомогою відомих відповідностей переходимо до зображаючого рівняння в просторі зображень;

2) розв’язуємо зображаюче рівняння, яке є алгебраїчним рівнянням першого степеня відносно . Одержимо зображення шуканого розв'язку;

3) користуючись одним із наведених в розділі 5 методів, визначаємо оригінал за зображенням .

Приклад 26. Розв’язати диференціальне рівняння

при початкових умовах .

Розв’язання. Припустимо, що , тоді . Таким чином, зображаюче рівняння має вигляд:

,

,

.

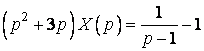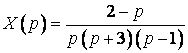Скористуємося теоремою (5.3).

Точки є простими полюсами.

.

.

.

.

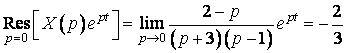Приклад 27. Розв’язати рівняння

.

Розв’язання. Для функції знайти зображення важко, тому будемо розв’язувати рівняння за допомогою інтеграла Дюамеля.

Спочатку розв'яжемо задачу Коші для рівняння:

.

.

.

.

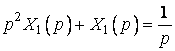За формулою (29) маємо

.

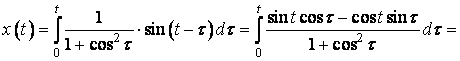
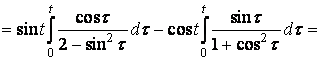
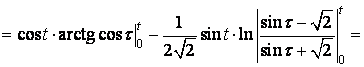
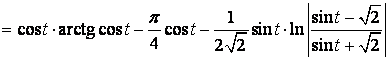Зауваження. Якщо початкові умови задані при довільному (а не при ) можна зробити заміну змінної, розв’язати одержане рівняння, а потім повернутися до старої змінної.

Приклад 28. Розв’язати рівняння

.

Розв’язання. Нехай і . Одержимо рівняння

.

.

.

.

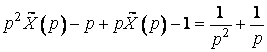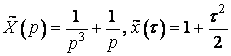Замінимо на . Одержимо

.

< Предыдущая		Следующая >