14. Зображення періодичних оригіналів

Нехай - періодичний оригінал з періодом , тобто для усіх .

Теорема. Зображення періодичного з періодом оригіналу визначається за формулою

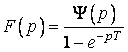, (26)

де 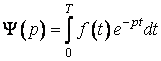. (27)

Функція, що визначається формулою (27), є зображенням оригіналу

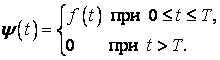
Приклад 19. Знайти зображення прямокутного імпульсу з періодом .

Рис. 15

Розв’язання. Запишемо функцію і знайдемо її зображення

.

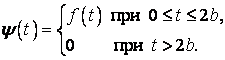
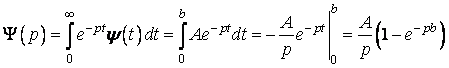За формулою (26) при одержимо

.

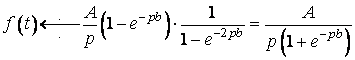Приклад 20. Знайти зображення періодичного оригіналу

(випрямлена синусоїда).

Рис. 16

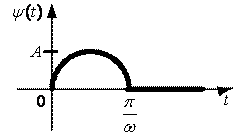
Рис. 17

Розв’язання. Функція має період .

Функція

.

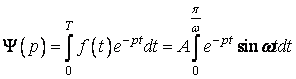Застосовуючи двічі інтегрування частинами, одержимо

.

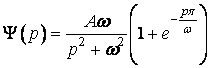За формулою (26) зображення функції має вигляд:

.

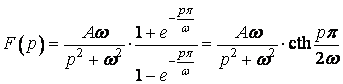Зауваження. Використали формули:

;

.

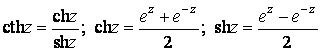Приклад 21. Знайти зображення функції, поданої на рисунку 18.

Рис. 18

Розв’язання. Період функції (Рис. 18) дорівнює 2.

Функцію (Рис. 19) можна записати так:

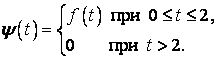
Рис. 19

Запишемо функцію за допомогою одиничної функції Хевісайда

;

.

Розділ 5. Знаходження оригіналу за даним зображенням

При розв’язанні цієї задачі треба використовувати одержані раніше відповідності функцій – оригіналів і їх зображень.

< Предыдущая		Следующая >