08. Разрешимые и перечислимые множества (языки)

Язык (множество слов) называют Алгорифмически разрешимым, если может быть построен нормальный алгорифм над алфавитом такой, что для каждого имеет место и .

Алгорифм , фигурирующий в вышеприведенном определении, называют Разрешающим алгорифмом для языка .

Легко показать, что, например, множество слов, содержащих хотя бы одно вхождение заданного непустого слова, будет алгорифмически разрешимо.

От ситуации возможности построения разрешающего НА для языка следует отличать ситуацию Полуразрешающего НА. Так называется НА , применимый к слову тогда и только тогда, когда . Принципиальное отличие от разрешающего НА состоит в том, что разрешающий всегда заканчивает работу за конечное число шагов, и мы рано или поздно получим ответ на вопрос о принадлежности слова языку. Что же касается полуразрешающего НА, то неизвестно, остановится он когда-нибудь и, следовательно, будет ли вообще дан ответ на вопрос о принадлежности.

Интуитивно очевидно, что из невозможности построения полуразрешающего НА следует невозможность построения и разрешающего. Докажем это строго.

Теорема 5. Если для языка Невозможен полуразрешающий НА, то невозможен и разрешающий.

Доказательство. Предположим противное, то есть предположим, что для языка Не может быть построен полуразрешающий НА, но возможно построение разрешающего. Пусть - такой НА. Тогда по теореме разветвления (теорема 3), построим НА

.

Ясно, что для любого слова имеет место , и НА является полуразрешающим вопреки предположению.

Образно говоря, разрешающий алгорифм можно «испортить», сделав его полуразрешающим.

Определим теперь понятие перечислимого множества (языка). Здесь нам понадобится понятие Конструктивного натурального числа (КНЧ). По определению, это любое слово в алфавите вида .

Язык (множество слов) называют Алгорифмически перечислимым, если существует нормальный алгорифм над алфавитом такой, что для каждого натурального числа N имеет место , и для каждого осуществимо такое натуральное число , что .

В дальнейшем будем говорить просто о разрешимых и перечислимых языках.

Понять смысл определения перечислимого языка будет проще, если вспомнить классическое теоретико-множественное понятие нумерации множества.

Именно, под Нумерацией множества понимается любое сюръективное отображение множества натуральных чисел на множество . Для простоты будем рассматривать далее только биективные (взаимно однозначные) нумерации. Можно показать, что это не ограничивает существенно общности. Множество в таком случае есть не что иное, как счетное множество.

Алгорифм называют при этом Алгорифмом, перечисляющим множество L (или просто Перечисляющим алгорифмом, если множество подразумевается). Говорят также, что Алгорифм перечисляет множество L. В свете теоретико-множественного понятия нумерации, перечислимое множество есть теоретико-алгоритмический (конструктивный) аналог понятия счетного множества, перечисляющий НА есть нумерация, заданная в виде нормального алгорифма, а осуществимость КНЧ в конце определения есть возможность задать в виде НА отображение, обратное нумерации (если последняя биективна).

Пример. Запишем НА, который перечисляет множество конструктивных целых чисел (КЦЧ). КЦЧ – это слово вида . Напишем сначала формулу обычной нумерации множества целых чисел:

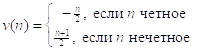
Соответствующий нормальный алгорифм строим по теореме разветвления:

,

Где - НА проверки четности,

- НА деления пополам с переходом к противоположному числу ( ),

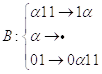- НА прибавления единицы и последующего деления пополам.

Может быть доказана следующая теорема:

Теорема 6. Всякое алгорифмически разрешимое множество алгорифмически перечислимо.

Заметим, что обратное неверно, что будет видно из дальнейших рассмотрений.

Легко понять также, что дополнение разрешимого языка также разрешимо.

В контексте проблемы применимости особенно важна характеристика перечислимых языков через области применимости нормальных алгорифмов.

Пусть дан НА над алфавитом . Областью применимости НА называется множество .

Теорема 7. Язык перечислим тогда и только тогда, когда он является областью применимости относительно алфавита некоторого нормального алгорифма.

Доказательство теорем 6 и 7 мы не приводим (см., например, [8]).

< Предыдущая		Следующая >