07. Универсальный нормальный алгорифм

Приступая к объяснению конструкции универсального НА, необходимо заметить следующее.

Очевидно, что наши действия по применению НА, заданного своей схемой, являются шагами некоторого алгоритма (в интуитивном смысле слова). Следовательно, согласно принципу нормализации, их можно задать некоторым нормальным алгорифмом. Он должен как-то воспринимать на входе любой НА и работать за него. Но для того, чтобы одни алгорифмы использовать в качестве исходных данных для других, необходимо алгорифм как данное, Превратить в конструктивный объект, то есть представить в виде слова в некотором алфавите. Существует два основных способа такой Конструктивизации нормального алгорифма: посредством Изображения и посредством Записи.

Пусть НА является алгорифмом в алфавите . Изображение НА есть слово в алфавите , где Которое строится по схеме следующим образом: формулы выписываются в порядке следования их в схеме, причем буква Служит разделителем между формулами, каждая стрелка заменяется буквой , а каждая точка – буквой .

Например, алгорифм левого присоединения слова , заданный схемой

,

Будет иметь изображение: .

Алгорифм правого присоединения непустого слова , заданный схемой в алфавите , где , имеющей вид (в сокращенной записи)

,

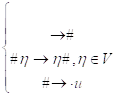Будет иметь такое изображение: , где предполагается, что .

В общем случае алгорифм, задаваемый схемой

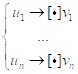
В алфавите , будет иметь изображение в виде слова .

Вместо изображения нормального алгорифма часто используют Запись нормального алгорифма – слово, определяемое как перевод изображения в алфавит . При построении записи НА в алфавите Принято считать, что буквы , фигурирующие в изображении, получают номера соответственно.

Так, запись алгорифма левого присоединения слова в алфавите Будет иметь вид .

Заметим, что в некоторых источниках буква в изображении НА пишется и в конце, то есть пишется сразу справа от изображения каждой формулы подстановки.

Запись нормального алгорифма будем обозначать.

Нетрудно понять, что как по изображению, так и по записи схема нормального алгорифма восстанавливается однозначно. Использование записи удобно в теоретических рассмотрениях, так как позволяет считать все нормальные алгорифмы представленными словами в одном и том же двухбуквенном алфавите (своего рода «двоичным кодом»).

Теорема 4 (теорема об универсальном нормальном алгорифме). Для любого алфавита И любого НА в этом алфавите может быть построен НА над алфавитом такой, что для любого слова имеет место условное равенство .

Алгорифм , построенный согласно данной теореме, называют Универсальным нормальным алгорифмом.

Существует вариант формулировки теоремы об универсальном алгорифме, в которой вместо записи фигурирует изображение «объектного» алгорифма .

Доказательство теоремы 4 чрезвычайно сложно и не может быть здесь рассмотрено. В курсе теории алгоритмов для студентов-программистов эта теорема также только формулируется.

Содержательный смысл теоремы состоит в том, что универсальный алгорифм получает на вход пару «объектный алгорифм – слово», декодирует запись объектного алгорифма, восстанавливая тем самым его схему, и применяет эту схему согласно известным правилам ко входному слову. Тем самым заданный в определении нормального алгорифма Алгоритм (определенный вне использования нормальных алгоримфов) применения схемы, согласно теореме об универсальном алгорифме сам может быть запрограммирован как Нормальный алгорифм.

С программистской же точки зрения универсальный алгорифм есть не что иное как Универсальный интерпретатор в классе программ, записанных в виде схем нормальных алгорифмов. Эту аналогию как раз важно провести в аудитории студентов-программистов. А именно, если пара (объектная программа , данные для нее ), то системная программа-интерпретатор , «декодируя» определенным образом объектную программу, сразу применяет ее к исходным данным. Это можно записать в виде условного равенства:

То есть интерпретатор выполняет функцию универсального алгоритма в некотором класса объектных программ.

< Предыдущая		Следующая >