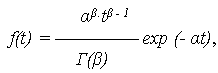Глава 07.2. Гамма–распределение

Случайная величина наработки до отказа T Имеет гамма-распределение с параметрами (масштабный параметр) и (параметр формы), где , > 0, причем – целое число, если ее ПРО описывается выражением:

(12)

 где Г() = ( - 1)! – гамма-функция Эйлера. Очевидно, что при = 1 выражение (12) упрощается до вида (1), соответствующего экспоненциальному распределению.

Гамма-распределение наиболее хорошо описывает распределение суммы независимых случайных величин, каждая из которых распределена по экспоненциальному закону.

При больших Гамма-распределение сходится к нормальному распределению с параметрами: a = · , b = · 2.

Графики изменения показателей надежности при гамма-распределении приведены на рис. 7.3.

Числовые характеристики наработки до отказа:

 - Средняя наработка (МО наработки) до отказа

T0 = / , (13)

(13)

 - Дисперсия наработки до отказа

D = D{T} = / 2 .

(14)

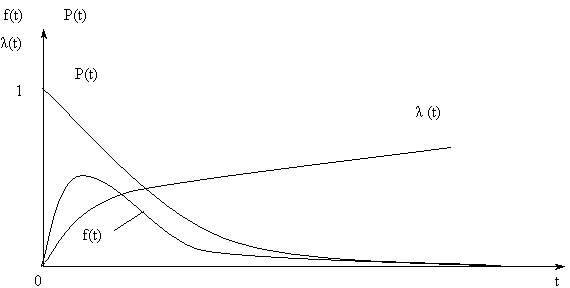
Рис. 7.3

 Помимо рассмотренных законов распределения, в качестве моделей надежности объектов могут использоваться и другие, например: распределение Вейбулла, хорошо описывающее наработку объектов до отказа по усталостным разрушениям, распределение Релея, распределение Эрланга и т. п.

< Предыдущая		Следующая >