11. Исчисление высказываний. Истинностные таблицы

Выше мы условились, что под высказыванием мы понимаем повествовательное предложение, которое имеет то свойство, что оно может быть классифицировано либо как истинное, либо как ложное, но не как то и другое вместе. «Истинность» или «ложность» предложения, которую мы приписываем высказыванию, и есть истинностное значение высказывания. Мы будем часто кратко обозначать «истинность» через Т и «ложность» через F. Если Р и Q — высказывания и связки употребляются в их обычном смысле, то каждое из предложений

~ Р, PQ, PQ, РQ, PQ

Есть высказывание. Рассмотрим вопрос подробнее.

Исходя из обычного значения слова «не», если высказывание истинно, то его отрицание ложно, и наоборот. Например, если S есть истинное высказывание (имеет истинностное значение Т) «Луна — спутник Земли», то ~ S ложно (имеет истинностное значение F).

По определению конъюнкция двух высказываний истинна тогда и только тогда, когда оба составляющих высказывания истинны. Например, «3 — простое число и 2 + 2 =5» —ложное высказывание, потому что «2 + 2 = 5» — ложное высказывание.

При условии, что связка «или» понимается в неразделительном смысле, обычное употребление квалифицирует дизъюнкцию как ложную тогда и только тогда, когда оба составляющих высказывания ложны. Приписывание истинных значений, которым мы занимаемся, может быть сведено в краткие истинностные таблицы, при помощи которых можно приписывать истинностное значение любому высказыванию для всех возможных случаев приписывания истинностных значений составляющим его высказываниям.

Ниже следуют истинностные таблицы для тех типов сложных высказываний, которые мы уже рассмотрели, а также для импликации и эквиваленции.

таб 1

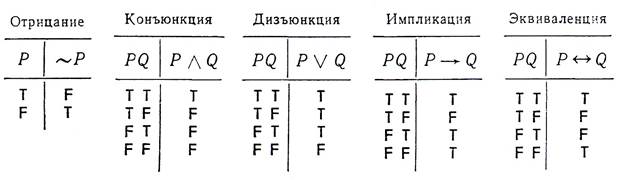
Таб.1

Обоснование истинностных значений, приписываемых импликации, состоит в том, что по интуитивному пониманию P→Q истинно тогда и только тогда, когда Q следует каким-либо образом из Р, Так, если Р истинно и Q ложно, то мы хотим, чтобы P→Q тоже было ложно; этим объясняется вторая строка таблицы. Далее, предположим, что Q истинно. Тогда естественно считать, что P→Q истинно, независимо от Р и его истинностного значения. Это рассуждение объясняет истинностные значения в первой и третьей строках таблицы. Чтобы обосновать четвертую строку таблицы, рассмотрим высказывание . Мы полагаем, что эта импликация будет истинна независимо от выбора Р и Q. Но, если Р и Q оба ложны, тогда РQ ложно; таким образом, мы вынуждены считать, что если и антецедент и консеквент ложны, то импликация истинна.

Таблица для эквиваленции определяется из таблиц для конъюнкции и импликации, исходя из того, что значит то же самое, что и

Эти пять таблиц должны пониматься как определения; это обычные определения, принятые в математике. Мы лишь попытались как-то согласовать их с естественным пониманием сентенциональных связок. Из этих определений непосредственно следует, что если Р и Q — высказывания, то ~ Р, PQ, PQ, РQ, PQ — тоже высказывания. Отсюда непосредственно вытекает, что каждое сложное предложение, чьи простые компоненты — высказывания, само есть высказывание.

Если истинностные значения простых компонентов известны, то истинностное значение сложного высказывания может быть определено механически.

Примеры

1. Предположим, что сложное высказывание символически записано

Так:

И что истинностные значения Р, Q, R и S будут Т, F, F и Т соответственно. Тогда значение есть Т, значение ~ S есть F, значение есть Т и, следовательно, значение первоначального высказывания есть Т, так как эта импликация имеет истинный антецедент и истинный консеквент. Такого рода вычисление можно сделать быстро, если написать под каждым простым высказыванием его истинностное значение, а истинностное значение каждого сложного высказывания — под соответствующей связкой. Итак, для приведенного выше сложного высказывания мы можем написать следующее (здесь в учебных целях последовательные шаги помещены на отдельных строчках, один под другим).

T F F T

T F

2. Рассмотрим следующее рассуждение.

«Если цены высоки, то и заработная плата высока. Цены высоки или применяется регулирование цен. Далее, если применяется регулирование цен, то нет инфляции. Наблюдается инфляция. Следовательно, заработная плата высока».

Предположим, что мы согласны с каждым из первых четырех высказываний (посылок). Должны ли мы согласиться с пятым высказыванием (заключением)? Чтобы ответить на этот вопрос, запишем сначала рассуждение символически, употребляя буквы Р, W, С и J вместо соответствующих высказываний. Так, Р есть предложение «Цены высоки». Тогда мы можем представить рассуждение следующим образом:

Предположение, что мы согласны с посылками, равносильно приписыванию значения Т всем высказываниям над чертой. Тогда поставленный вопрос может быть сформулирован так: если посылки имеют истинностное значение Т, имеет ли заключение значение Т? Ответ будет утвердительным. Действительно, если J и имеют значение Т, то значение С есть F согласно истинностной таблице для импликации. Следовательно, Р имеет значение Т (поскольку Имеет значение Т) и, следовательно, W имеет значение Т (поскольку имеет значение Т).

3. Рассмотрим конъюнкцию

Двух высказываний, приведенных в предыдущем примере. Вообще говоря, истинностное значение, которое получит такое высказывание, за-

Висит от значений, приписанных составляющим его простым высказываниям. Естественно предположить, что в период неустойчивых экономических отношений истинностное значение, приписываемое одному или нескольким из высказываний Р, С и J, будет меняться, переходя из Т в F или наоборот. Так, может возникнуть вопрос о комбинациях истинностных значений Р, С и J, для которых имеет значение Т или значение F. На это можно будет ответить при помощи таблицы, в которой приведено истинностное значение сложного высказывания для каждого возможного распределения (23) истинностных значений высказываний Р, С и J. Она называется истинностной таблицей для данного высказывания и приведена ниже. Каждая строчка включает в себя какое-либо из распределений истинностных значений высказываний Р, С и J вместе с соответствующим значением высказывания . Последнее может быть вычислено так же, как и в приведенном выше первом примере.

таб 2

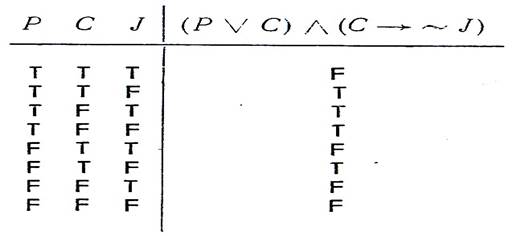
Таб.2

Однако при заполнении таблицы читатель, конечно, в самом процессе работы нащупает кратчайшие пути.

4. Если Р — «2 есть простое число» и L — «Логика — занятное дело», то никто не мешает нам построить сложные высказывания такого рода, как

Поскольку Р и L имеют истинностные значения (ясно, что оба есть Т), эти сложные высказывания тоже имеют истинностные значения, которые мы можем указать. Первая наша реакция на такой вздор — «нужно запретить такие построения», так как де образование конъюнкций, импликаций и т. д. следует допускать только в том случае, когда составляющие их высказывания связаны по своему содержанию или предмету. Однако не требуется долгих размышлений, чтобы понять, с какими трудностями связано определение столь неясных понятий. Гораздо проще пойти легким путем, т." е. допустить образование сложных высказываний из любых простых. С точки зрения смысла это иногда приводит к высказываниям, представляющим собой вздор, но вреда от этого не будет. Мы ведь заняты формулированием принципов правильного рассуждения. В приложении к систематическому рассуждению сложные высказывания, сводящиеся к нечленораздельной болтовне, просто не встречаются.

Упражнения

1. Предположим, что высказываниям Р, Q, R и S соответственно приписаны значения Т, F, F и Т. Найти истинностные значения каждого из следующих высказываний:

(a) (f)

(b) (g)

(d) (i)

(e) (j)

2. Составить истинностную таблицу для каждого из следующих высказываний:

(a) (d)

(b) (e)

3. Пусть значение высказывания P→Q есть Т. Что можно сказать о значении высказывания ?

4. а) Пусть значение высказывания есть Т; что можно сказать о значениях высказываний и ?

B) Пусть значение высказывания есть F; что можно сказать о значениях высказываний и ?

5. Для каждого из помещенных ниже высказываний определить, достаточно ли приведенных сведений, чтобы установить истинностное значение высказывания. Если достаточно, то указать это значение. Если

Недостаточно, то показать, что возможны и одно, и другое истинностные значения.

(a) (d)

T T

(b) (e)

T T

T T F

6. В третьем примере параграфа 2.1 мы записали символически высказывание

«Если рабочие или администрация упорствуют, то забастовка будет урегулирована тогда и только тогда, когда правительство добьется судебного запрещения, но войска не будут посланы на завод» в следующем виде:

Путем рассмотрения истинностных значений определить, истинно или ложно это высказывание при каждом из следующих предположений:

A) Рабочие упорствуют, а администрация нет, забастовка будет урегулирована, правительство добилось судебного запрещения и войска посылаются на завод.

B) И рабочие, и администрация упорствуют, забастовка не будет урегулирована, правительству не удалось добиться судебного запрещения, и войска посылаются на завод.

7. В связи с высказыванием в предыдущем примере примем следующее: «Если правительство добьется судебного запрещения, то на завод будут посланы войска. Если на завод будут посланы войска, то забастовка не будет урегулирована. Забастовка будет урегулирована. Администрация упорствует».

Определить, истинно ли высказывание из упражнения 6.

< Предыдущая		Следующая >