05. Примеры решения задач

Задача 1. Каждый из четырех студентов, проживающих в одной комнате общежития, может присутствовать или не присутствовать на лекции по теории вероятностей. Рассматриваются события:

A - На лекции присутствует ровно один из четырех студентов ;

B - На лекции присутствует хотя бы один из четырёх студентов;

C - На лекции присутствуют не менее двух из четырех студентов;

D - На лекции присутствуют ровно два из четырех студентов;

E - На лекции присутствуют ровно три из четырех студентов;

F - На лекции присутствуют все четыре студента.

Решение: Начинать решение нужно с построения пространства элементарных исходов (элементарных событий) рассматриваемого эксперимента. Вспомним, что таким пространством называется любое множество W взаимоисключающих исходов эксперимента такое, что каждый интересующий нас результат эксперимента может быть однозначно описан с помощью элементов этого множества. В данном случае случайный эксперимент заключается в наблюдении за четырьмя студентами и выяснении, посещают ли они лекции по теории вероятностей. Нас интересует только количество студентов, присутствующих на лекции. Пусть элемент описывает элементарный исход, означающий, что на лекции присутствовало ровно i студентов. Тогда Все случайные события формально есть подмножества множества описаний элементарных исходов. Выпишем формально все события, о которых идет речь в условии задачи. Для этого нужно перечислить описания элементарных исходов, благоприятствующих каждому из этих событий. Таким образом будем иметь: Применяя теоретико-множественные операции для множеств получим ответ задачи. Ответ: а)

Г)

Е)

Задача 2. Пусть прибор состоит из трех блоков первого типа и двух блоков второго типа. Для того, чтобы прибор работал нормально необходима исправность хотя бы двух блоков первого типа и хотя бы одного блока второго типа. Пусть события означают исправность блока первого типа при События означают исправность блока второго типа при Используя теоретико-множественные операции записать событие , означающее что прибор исправен.

Решение: Для наступления события на самом деле необходимо наступление двух событий . Событие значит, что исправны хотя бы два блока первого типа. Событие значит, что исправен хотя бы один блок второго типа. Таким образом получим Осталось записать события И . Событие Наступает в случае, если одновременно наступают и , т. е. имеет место событие Ç, или если одновременно появятся И , или одновременно наступают и . При этом не исключается случай одновременного наступления всех трех событий , и . Таким образом используя определения операций объединения и пересечения событий, получим Заметим, что событие , означающее одновременное появление , и , содержится в каждом из трех объединяемых событий в выражении для . Аналогично запишем Ответ: .

Задача 3. Используя законы для операций над событиями доказать справедливость следующего равенства:

Решение. Пользуясь свойством г) для операций над событиями запишем: Далее, используя закон де Моргана и первый распределительный закон, получим:

Что и требовалось доказать.

Задача 4. Используя определения операций над событиями доказать, что .

Решение: Для решения задачи достаточно показать выполнение двух включений: 1) Докажем первое включение, второе доказывается аналогично. Будем предполагать, что в противном случае первое включение очевидно. Выберем некоторый элементарный исход Покажем, что тогда Пусть Тогда по определению разности событий запишем:

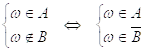. Далее по определению операции пересечения событий и получаем, что Что и требовалось доказать.

< Предыдущая		Следующая >