02. Примеры решения задач

Задача 1. Нужно составить комиссию из трех равноправных членов, выбирать представителей комиссии можно из четырех семей (муж и жена), причём от каждой семьи не может избираться более одного человека.

Решение. Операция - составление комиссии может быть представлена как последовательное выполнение четырех действий. Действие - выбор трех семей, члены которых будут представлены в комиссии. Это можно сделать различными способами. Действие - выбор одного человека (мужа или жены) в одной из семей, представленной в комиссии, это действие выполняется =2 различными способами. Действия и - выбор по одному представителю из двух других семей, члены которых включаются в комиссию. Каждое из действий и выполняется также двумя различными способами, т. е. Окончательно получаем и такую комиссию можно составить 32 различными способами. Ответ: 32.

Следует заметить, что действия , выбирались таким образом, что изменение результата любого из них ведет к новому составу комиссии.

Рассмотрим другое решение этой задачи. Операцию А представим в виде последовательного выполнения действий . Действие Означает выбор в каждой из четырех семей по одному члену. Затем выполняется действие , заключающееся в выборе трех членов комиссии из четырех, отобранных в результате выполнения . Действие может быть выполнено различными способами, действие выполняется различными способами. В результате имеем различных вариантов комиссии. Ответы не совпали. Почему? Всё дело здесь в том, что неверно применёно правило умножения. Можно изменить результат действия и получить опять тот же состав комиссии. Поясним сказанное на конкретном примере. Пусть есть четыре семьи. Перечислим их членов по именам и результат действий и изобразим на следующей схеме:

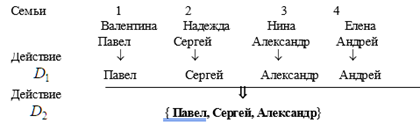В данном примере результат первого действия – это выбор Павла, Сергея, Александра и Андрея. Результат второго действия и есть комиссия в составе Павла, Сергея и Александра. Но можно изменить результат действия , выбрав на первом этапе Павла, Сергея, Александра, Елену, и получить тот же состав комиссии. При этом на втором этапе опять же выбираем Павла, Сергея, Александра как показано на следующей схеме :

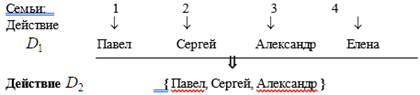Таким образом, изменение результата действия не привело к изменению результата всей операции.

Задача 2. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если: а) ни одна из цифр не повторяется; б) цифры могут повторяться?

Решение: А) Можно решать данную задачу с использованием основного правила комбинаторики. Процесс составления четырехзначного числа можно разбить на четыре последовательных действия: - выбор первой цифры, - выбор второй цифры, - выбор третей цифры, - выбор четвертой цифры. На первом месте в числе может стоять одна из шести цифр 1, 2, 3, 4, 5, 6. Если первая цифра выбрана, то на второе место может быть поставлена любая из шести оставшихся цифр (второй цифрой может быть и ноль). После выбора первых двух цифр, третья выбирается пятью различными способами. Если первые три цифры в числе известны, то четвертую можно выбрать четырьмя различными способами. В результате Ответ: 720.

Можно решать эту задачу и используя стандартные комбинации. В данном случае подойдут размещения без повторений. Посчитаем сначала, сколько различных векторов можно составить, если все компоненты вектора различны и могут быть цифрами 0,1,2,3,4,5,6. Всего таких векторов . Далее посчитаем сколько существует различных векторов , у которых , а все другие компоненты различны и могут быть цифрами 1,2,3,4,5,6. Таких векторов . Четырехзначных чисел, удовлетворяющих условиям задачи будет столько, сколько можно составить различных векторов , у которых все компоненты различны, могут принимать значения 0,1,2,3,4,5,6 и Таких векторов - = 720. Ответ: 720.

Б) Для данного варианта задачи опять предложим два способа решения. Основное правило комбинаторики используется аналогично п. а). В данном случае

С использованием стандартных комбинаций получим: Ответ: 2058.

Задача 3. Сколько различных пятизначных чисел можно составить из цифр 1,2,3,4,5,6,7, если есть одна цифра, которая повторяется в числе ровно два раза, а все другие цифры разные?

Решение: Процесс составления числа, удовлетворяющего условию задачи представим в виде последовательного выполнения следующих действий: - выбор цифры, которая будет повторяться два раза; - выбор двух мест в пятизначном числе для повторяющейся цифры, - выбор и расстановка трех разных цифр из оставшихся на три свободные места в пятизначном числе. Здесь получаем Ответ: 8400.

Задача 4. Сколькими различными способами можно разложить в различных ящиков Белых и чёрных шариков, если в каждом ящике может находиться любое количество шариков, некоторые ящики могут оставаться пустыми?

Решение: Операцию размещения шариков по ящикам разобьем на два последовательных действия: - распределение белых шариков; - распределение чёрных шариков по ящикам. Так что достаточно вычислить каким числом способов может быть выполнено каждое из действий, а далее использовать основной закон комбинаторики.

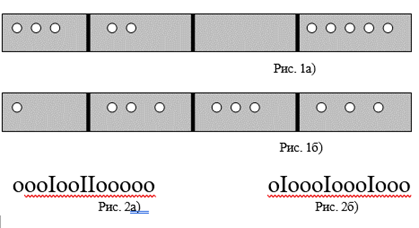
Посчитаем количество различных разложений белых шариков по ящикам. На рис. 1а) и 1б) изображены два различных расположения белых шариков по ящикам. Нетрудно видеть, что разложения шариков, изображенные на рис. 1а) и 1б), можно однозначно описать с помощью цепочки шариков и палочек, как это сделано на рис. 2а) и 2б). Если ящиков , а белых шариков , то в этой цепочке будет (-1) палочка и Шариков. Так что различных разложений белых шариков будет столько, сколько можно составить различных цепочек длины из палочек и шариков. А таких цепочек столько, сколькими различными способами можно выбрать мест в цепочке под шарики, т. е. Таким образом получим

Аналогично подсчитывается число различных разложений черных шариков по ящикам, . Количество распределений всех шариков по ящикам согласно основному закону комбинаторики будет равным Ответ:

Задача 4 может быть решена и с использованием стандартных комбинаций. Процесс распределения белых шариков по ящикам может быть выполнен следующим образом. Берем белый шарик и выбираем для него любой из n ящиков, далее берем следующий белый шарик, опять выбираем для него любой из n ящиков и т. д., процедуру повторяем r раз. Т. е. для каждого шарика выбираем ящик, причем каждый ящик может быть выбран несколько раз. Если некоторый ящик выбрали q раз, то это означает, что в нем окажутся q шариков. Различных распределений белых шариков по ящикам ровно столько, каким числом способов можно выбрать из n ящиков r ящиков с повторениями, т. е. Число различных разложений всех шариков (белых и чёрных) по ящикам будет ровно Решая эту задачу двумя различными способами получаем формулу для вычисления числа различных сочетаний из по с повторениями.

< Предыдущая		Следующая >