8.1 Решение обыкновенных дифференциальных уравнений. Метод численного интегрирования
Рассмотрим задачу Коши для обыкновенного дифференциального уравнения первого порядка:
![]() =F(X,Y), Y(A)=Y0; XÎ [A,B]. (8.1)
=F(X,Y), Y(A)=Y0; XÎ [A,B]. (8.1)
Интегрируя (8.1), заменим эту задачу эквивалентным ей интегральным уравнением типа Вольтера:
Y(X)= Y0 + ![]() F(T,Y(T)) Dt. (8.2)
F(T,Y(T)) Dt. (8.2)
Решим уравнение (8.2) методом последовательных приближений. В результате получим итерационный процесс
Y(k)(x) = y0 + ![]() F(t, y(k-1)(t)) dt, (8.3)
F(t, y(k-1)(t)) dt, (8.3)
Зададим сетку Xi=A+Ih; I=0,…,M, где H=![]() - шаг сетки. Из уравнения (8.3) имеем
- шаг сетки. Из уравнения (8.3) имеем
Y(k)(xi) = yi(k) = y0 + ![]() F(t, y(k-1)(t)) dt, (8.4)
F(t, y(k-1)(t)) dt, (8.4)
Где Y(0)(T)=Y0.
Интеграл в правой части (8.4) вычисляется с помощью численной квадратуры
Yi(k) –Y0 = H![]() Aj(i) F(xj, yj(k-1)) . (8.5)
Aj(i) F(xj, yj(k-1)) . (8.5)
Коэффициенты Aj(I) системы (8.5) находятся из решения системы линейных алгебраических уравнений:
![]() =
= ![]() Aj(I) Jk-1; K=1,…N+1;I=1,…N . (8.6)
Aj(I) Jk-1; K=1,…N+1;I=1,…N . (8.6)
Система (8.6) получена из условия, что формула (8.5) точна для всех функций вида X, X2, X3,…, Xn+1 в точках Xi = Ih, I=0,…,N.
Пусть N=2, дано три точки (X0,X1,X2). Тогда матрица коэффициентов Aj(I) равна
A= .
.
Для M=4 , пять точек (X0, X1, X2, X3, X4).
A=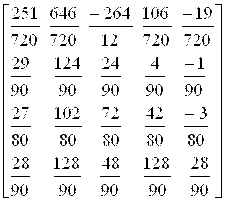 .
.
Численная реализация может быть выполнена следующим образом.
Шаг 1. Исходный интервал делим на 4 части, т. е. задаем M = 4. Определяем сетку Xi=A+Ih0, I=0,1,…,4, где H0 = (A+B)/4 - шаг исходной сетки. Вычисляем по формулам (8.5) Yi(N), I=1,…,4 , пока не выполнится условие max![]() <E, по всем I, где E - заданная точность.
<E, по всем I, где E - заданная точность.
Шаг 2. Делим интервал на 8 частей, т. е. уменьшаем шаг вдвое и находим Yi На сетках:
![]() =A+ih1, i=1,…,4; H1=h0/2;
=A+ih1, i=1,…,4; H1=h0/2;
![]() =(b+a)/2+ih1, i=1,…,4.
=(b+a)/2+ih1, i=1,…,4.
Затем проверяем условие max![]() <E в узлах первой сетки (с шагом H0). Если оно выполняется, то вычисления заканчиваем. Если не выполняется, то исходный интервал уменьшаем вдвое, т. е. A1=A; B1=(A+B)/2, и переходим на шаг 1, где A=A1; B=B1.
<E в узлах первой сетки (с шагом H0). Если оно выполняется, то вычисления заканчиваем. Если не выполняется, то исходный интервал уменьшаем вдвое, т. е. A1=A; B1=(A+B)/2, и переходим на шаг 1, где A=A1; B=B1.
| < Предыдущая | Следующая > |
|---|