4.3. Метод пропорционального деления (метод хорд)

Выберем неподвижным тот конец отрезка, для которого знак функции F(X) совпадает со знаком ее второй производной F"(X). Тогда последовательные приближения Xn лежат по ту сторону корня X, где функция F(X) имеет знак, противоположный знаку ее второй производной F"(X).

Например, если F"(X)>0 при A £ x £ b, То кривая Y=f(X) будет выпукла вниз.

Возможны два случая:

1) F(A)>0, тогда X0=b (рис. 4.5) и неподвижен конец A,

Xn+1= Xn- (N=0, 1, 2,…);

2) F(A)<0, тогда X0=A (рис. 4.6) и неподвижен конец B,

Xn+1= Xn - (N=0, 1, 2,…).

Этот метод имеет линейную сходимость, есть погрешность на (n+1) - й итерации пропорциональна погрешности на n -й итерации. В этом случае говорят, что метод первого порядка точности.

Для оценки погрешности N-го приближения корня можно воспользоваться формулой | Xn-X | £ или | Xn-X | £ |Xn - xn-1|,

Где M1 = Min | F'(X)| , M1 =Max| f’(X)| для всех x[A, B].

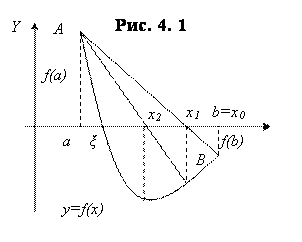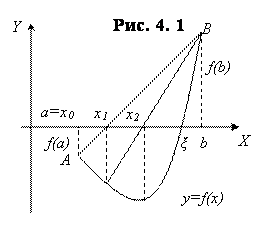< Предыдущая		Следующая >