3.5. Задания

1. Вычислить приближенное значение интеграла 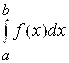, используя формулы трапеции, Симпсона, трех-восьмых, прямоугольников и Гаусса (N=4, 5 Или 7). Оценить остаточный член формул.

2. Вычислить значение интеграла 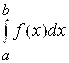с заданной точностью e, используя формулу трапеции или Симпсона, двумя способами:

- выбрать шаг интегрирования из оценки остаточного члена,

- использовать метод последовательного удвоения числа шагов.

3. Вычислить значение интеграла 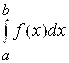с заданной точностью e, если функция F(X) имеет разрыв второго рода.

4. Вычислить значение интеграла 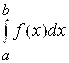, заменив функцию F(X) кубическим сплайном.

5. Вычислить двойной интеграл .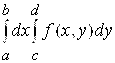

Варианты

Для заданий 1,2,4:

1. F(X)=x3 E2x ; a=0 ; b=1.

2. F(X)= ; a=0 ; b=4.

3. F(X)=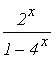 ; a= -2 ; b= -1.

4. F(X)=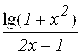 ; a=0 ; b=1.

5. F(X)=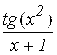 ; A=0 ; b=1.

6. F(X)= ; a=1 ; b=3.

7. F(X)=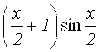 ; a=1 ; b=2.

8. F(X)=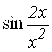 ; a=0,5 ; b=2,5.

9. F(X)= ; a=5 ; b=7.

10.F(X)= ; a=0 ; b=5.

11.F(X)=cos(x)/(x+2) ; a=0,4 ; b=1,2.

12.F(X)= ; A=0,4 ; b=1.2.

13.F(X)=(x+1)sin(x) ; A=1,6 ; b=2.4.

14.F(X)=(x+1)cos(x2) ; a=0,2 ; b=1.

15.F(X)=sin(x2-0,4)/(x+2) ; a=0,8 ; b=1,2.

16.F(x)=ln(1+x2)/(1+x2) ; a=0; b=1.

17.F(x)=ln(5+4cos(x)) ; a=0; b=3,1416.

18.F(x)=x*ln(1+x); A=0; b=1.

Для задания 3:

1. F(X)= ; A= 0; b= 0,5.

2. F(X)= ; a= 0; b= 1.

3. F(X)= ; A= 0; b= 1.

4. F(X)= ; a= 0; b= 2.

5. F(X)=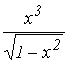 ; A= 0; b= 1.

6. F(X)=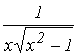 ; a= 1; b= 2.

7. F(X)=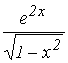 ; A= -1; b= 1.

8. F(X)= ; a= -1; b= 1.

9. F(X)=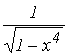 ; A= -1; b= 1.

10.F(X)= ; A= 0; B= 1.

Для задания 5:

1. .

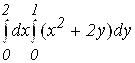2. .

3. .

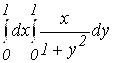4. .

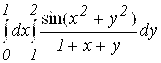5. .

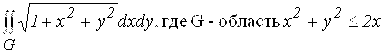6. .

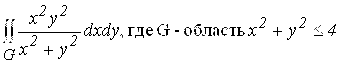7. 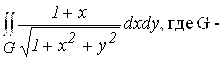Правильный шестиугольник, вписанный в единичный круг.

8. .

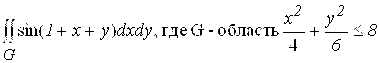9. .

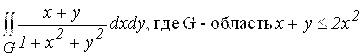10.Ромб с центром в начале координат и с вершинами в точках (0, -4); (0, 4); (-2, 0); (2, 0).

< Предыдущая		Следующая >