3.2. Квадратурные формулы

Пусть для функции Y=f(X) требуется вычислить интеграл J(F)=.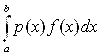

Выбрав шаг H=, Разобьем отрезок [A, b] на N равных частей: X0=A, Xi=X0+Ih ( I=1, 2,…, N-1), Xn=B И пусть Yi=f(Xi) ( i=0, 1, 2, …, n), P(X) =1.

Построим, например, полином Лагранжа:

F(X) ≈ L N (X) = +R N (X) .

Заменяя функцию F(X) Соответствующим интерполяционным полиномом, получим квадратурную формулу

,

Где Ai - Некоторые постоянные коэффициенты, не зависящие от функции F(X), а зависящие лишь от расположения узлов сетки Xi.

Для формулы трапеции (N=1) P(X)=1, A0=A1=1/2.

=(Y0+y1).

Остаточный член формулы трапеции равен:

R=-(Y0+Y1)=,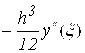

Где ξ(X0, x0+h).

Обобщенная формула трапеции для вычисления определенного интеграла на равномерной сетке, запишется так:

,

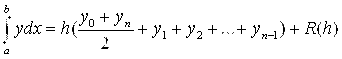Где R(H)=, М2=.

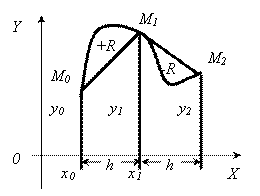Формула Симпсона при N=2 и P(X)=1. Интерполирование функции выполняется по трем ее значениям. A0=1/6, A1=2/3, A2=1/6 Или, так как X2-x0=2h,

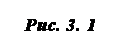
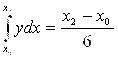(Y0+4Y1+Y2).

Остаточный член формулы Симпсона равен

R=-(Y0+4Y1+Y2)= ,

Где ξ(X0,x2).

Обобщенная формула Симпсона для вычисления определенного интеграла на равномерной сетке и четного числа шагов, имеет вид:

,

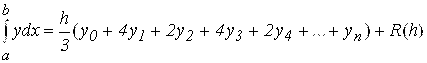Где R(H)=, М4=.

Приведем формулу «трех восьмых» для вычисления определенного интеграла на равномерной сетке и числа шагов, кратного трем:

,

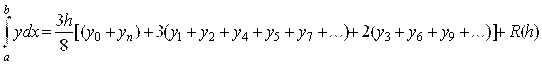Где R(H)=, М4=.

Задание. Вывести обобщенную формулу трапеции , заменив подынтегральную функцию F(X) линейным интерполяционным многочленом

F(X)=Yi+(Yi+1-Yi)

На каждом отрезке [Xi, xi+1] (I=0, 1,…, n-1), А формулу Симпсона получить, заменив подынтегральную функцию F(X) квадратичным интерполяционным многочленом

F(X)=Yi+(Yi+1-Yi)

На каждом отрезке [Xi, xi+2] (I=0, 2, 4,…, n-2).

Самостоятельно получить формулы прямоугольника из вида площади на графике (рис.3.3). Вывести отдельно левую, правую и центральную формулы и их погрешности.

< Предыдущая		Следующая >