3.1. Численное интегрирование. Постановка задачи интегрирования

Численное интегрирование функции целесообразно использовать в тех случаях, когда: 1) первообразная F(X) не может быть найдена с помощью элементарных функций; 2) F(X) является слишком сложной; 3) подынтегральная функция F(X) задана таблично или неявно.

Будем рассматривать формулы приближенного вычисления интегралов

, где P(X) >0 - заданная интегрируемая функция (весовая) и F(X) - достаточно гладкая функция, xÎ[A,B] и Ck - числа, K=0,1,…,n..

Для составления квадратурных формул данную функцию F(X) заменяют интерполирующей функцией φ(X) И приближенно полагают

≈

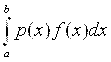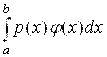
И затем вычисляют интеграл непосредственно, а оценку погрешности формулы определяют исходя из вида функции F(X).

< Предыдущая		Следующая >